Reference no: EM13648109

Define the language L to consist of strings that represent certain web-page addresses. For this assignment you are to design a DFA to recognize L and write a program that implements your DFA.

The Language L

To precisely specify L, first define Γ = {a, b, c, . . . , z} as the set of lower-case Roman letters, and let Σ = Γ ∪ {.}; i.e., Σ is the set consisting of all the lower-case Roman letters and the dot (or period). Define the following sets:

S₁ = {www.}

S₂ = ΓΓ∗, which consists of strings over Γ of positive length

S₃ = {.com} ∪ {.co.jp}

Then we define the following sets of strings over Σ:

L₁ = S₁S₂S₃

L₂ = S₂S₃

L = L₁ ∪ L₂

Strings in L₁ are (a subset of) web addresses that have three parts, where the first part is "www.", the second part is a positive-length string of lower-case Roman letters, and the third part is ".com" or ".co.jp". (The suffix ".co.jp" is used in some web addresses in Japan.) Strings in L₂ are (a subset of) web addresses that have only the last two parts. For example, the strings www.abcdef.com, www.com.com, www.co.com, www.abcdef.co.jp, www.com.co.jp, and www.co.co.jp belong to L1, and the strings abcdef.co.jp, www.co.jp, abcdef.co.jp, and www.co.jp belong to L2.

The specification of L does not include all valid web addresses since we included several restrictions to simplify the assignment. For example, only lower-case Roman letters and dots are allowed, strings in L must end with .com or .co.jp, etc.

DFA for L

First construct a DFA M = (Q, Σ, δ , q1, F ) that recognizes L. The DFA must satisfy each of the following properties:

The DFA must be defined with the above alphabet Σ. Your DFA does not have to handle symbols that are not in Σ.

The states in the DFA must be labeled q₁, q₂, q₃, . . . , q_n, where q₁ is the start state and n is the number of states in the DFA. (It is also acceptable for the states to be labeled q₀, q₁, . . . , q_n-1, with q₀ the start state.)

You will lose points if your DFA is overly complicated. To simplify your DFA drawing, omit any edges going from a state q ?∈F to a "trap state" (i.e., a non-accepting state from which the DFA can never leave). All other edges must be included in your drawing. Clearly identify which state is the trap state in the drawing of your DFA. Also, to simplify your drawing, you should define Γl = Γ - {l} for any symbol l ∈ Γ; i.e., Γl is the set of all lower-case Roman letters except for l. For example, Γw = {a, b, c, . . . , v, x, y, z}, so your DFA might include something like the following:

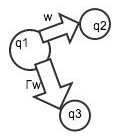
Thus, if the DFA is currently in state q₁, then it moves to q₂ on reading w, and it moves to state q₃ on reading any other lower-case Roman letter.

Program Specifications

You must write your program in either C, C++, or Java. All input/output must be through standard input/output, and your program is to work as follows:

1. Your program asks the user if s/he wants to enter a string. The user then enters "y" for "yes", or "n" for "no".

If the user enters "n", then the program terminates.
If the user enters "y", then the user is prompted to enter a string over Σ.

2. If the user chooses to input a string, your program then reads in the string. After reading in the string, your program prints it. Then your program processes the entire string on the DFA, one character at a time, in the following manner.

Your program must begin in the start state of the DFA and print out the name of that state (q1 or q0).

After each character from the string is processed on the DFA, your program must print out the character and the name of the current state of the DFA. Even if your DFA is in a trap state, your program must do this for each character in the string until it reaches the end of the string.

To simplify your program, you should check the ASCII code of each character of the string and process on the DFA accordingly.

3. After processing the entire string on the DFA, your program must indicate if the string is accepted or rejected based on the state in which the DFA ended. Your program then should return to step 1.