Reference no: EM131144457

Q1. A grounded, homogeneous, uncharged metal sphere of radius a is placed into a uniform electric field E₀ directed along the z axis as shown below. The sphere is centered on the origin.

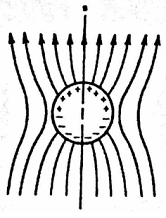
The electric potential outside the sphere obeys the Laplace PDE In spherical coordinates.

∇²ψ = 0

(a) Due to symmetry, we can assume that there is no cp variation or dependence. Under this assumption, show that the solution to the Laplace PDE in the region outside the sphere is:

ψ = ∑_n(a_nrⁿ + b_nr^-(n+1)P_n(cosθ), Hint - Use -n(n+1) as an expansion constant for θ. 

(b) The boundary condition for this situation requires that ψ = 0 when r = a. Show that this condition reduces the solution for the potential to:

Ψ = -E₀rP₁(cosθ)(1-(a³/r³))

HINT - Far from the sphere when r >> a, the potential must replace to that due to the field alone:

ψ = -E₀z = -E₀rcosθ

Use this information in the limit that r is large to eliminate a whole bunch of constants from the solution in (a). Then apply the boundary condition and see what other constants you can get rid of or solve for.

Q2. Consider the diffusion equation shown below describing the concentration of electrons in an electronic device:

2 ∂²n/∂x² = ∂n/∂t

0 < x < l, t > 0

For t = 0, n(1, 0)=5 and zero for all other values of x. In other words, your initial "n" vector at t=0 should look like (0 0 0 0 5 0 0 0 0)^T

Use a stable numerical method to estimate the solution to this equation at t = 0.025 sec over the interval 0 < x < 2 with 10 steps along x and k = .001.

Q3. SPPARATION OF A FOURTH-ORDER PDE. VIBRATING BEAM

By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniforms elastic beam are modeled by the fourth-order PDE.

(21)  ∂²u/∂t² = -c² ∂⁴u/∂x⁴

where c2 = EI/ρA (E = Young's modulus of elasticity, I = moment of inertia of the cross section with respect to the y-axis in the figure, ρ= density, A = cross-sectional area).

1. Substituting u = F(x)G(t) into (21), show that

F(4)/F = -G^··/c²G = β⁴ = const,

F(x) = A cosβx + B sin βx + D cosh βx + D sinh βx,

G(t) = a coscβ²t + bsin cβ²t.

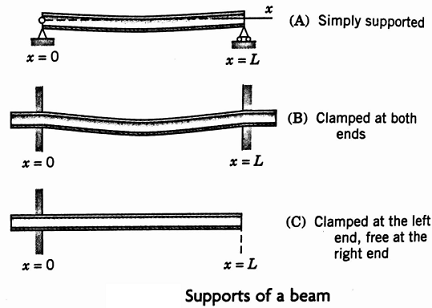
2. Simply supported beam in Fig. Find solutions u_n = F_n(x)G_n(t) of (21)  corresponding to zero initial velocity and satisfying the boundary conditions.