Reference no: EM131018229
1: A bank branch located in a commercial district of a city has developed an improved process for serving customers during the noon-to-1:00 p.m. peak period. The waiting time in minutes (defined as the time customer enters the line to the time he/she is served) of all customers during this hour is recorded over a period of one week. A random number sample of 15 customers is selected, and the results are as follows:
|
4.21
|
5.55
|
3.02
|
5.13
|
4.77
|
2.34
|
3.54
|
3.20
|
|
4.50
|
6.10
|
0.38
|
5.12
|
6.46
|
6.19
|
3.79
|
|
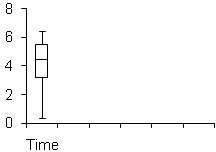
a) Describe the shape of the distribution of the bank branch located in a commercial district of a city using the information from a) - c).
Answered:Here, we are able to show the shape of the distribution, its central value, and its variability. The distribution of the waiting time in minutes is mostly skewed to higher end with the median at 4.50 due to the higher waiting time averages on the 4 plus minutes. The whiskers are extending almost all the way towards 7 minutes from less than a minute.
b) Explain why you would think that the shape you describe above in a) happens with this type of data.The type of data is a collection of waiting times at a local bank in a commercial district during a lunch time. If you were one of these customers, what shape would you expect for a boxplot of waiting times?
2: The Corner Convenience Store kept track of the number of paying customers it had during the noon hour each day for the last 150 days. The following are the resulting statistics rounded to the nearest integer:
|
 sample mean) = 95 sample mean) = 95
|
s (sample standard deviation) = 12
|
|
 (median) = 97 (median) = 97
|
Q1 (first quartile) = 85
|
|
m (mode) = 99
|
Q3 (third quartile) = 107
|
|
R(range) = 56
|
|
a) For how many of the 150 days was the number of paying customers within three standard deviations from the mean? Explain how you determined your answer.
b) For how many of the 150 days was the number of paying customers within three standard deviations from the mean? Explain how you determined your answer. Since the median is larger than the mean, the shape of the data is NOT bell-shaped. Hence the Empirical Rule is not applicable. Use given descriptive measures.