Reference no: EM131108865
2009 Honors Examination in Algebra
[1](a) Let H be a subgroup of a finite group G. Show that the number of conjugates gHg-1 of H in G divides the index [G: H] of H in G.
(b) Now let G act on the left on a set X, and consider the orbit Ox = {gx | g ∈ G} of an element x ∈ X. Let Gx = {g ∈ G | gx = x} denote the stabilizer (isotropy subgroup) of x. Are all of the subgroups Gy for y ∈ Ox conjugate to Gx? Does this list include every subgroup conjugate to Gx? Does each distinct subgroup appear the same number of times?
(c) A recurring theme in group theory is that we need look no further than the group G itself, to understand questions like the above. Can you construct a set Y from G itself which admits a left action by G, and has an orbit with the same structure as Ox above?
[2](a) Classify the finite groups of order 12.
(b) Two groups are the nonsingular matrices of the form A with integer entries mod 2, and the nonsingular matrices of the form B with integer entries mod 3, where
Which groups are they?
[3](a) Construct explicitly the finite field F25 of order 25, as a quotient F5[x]/(f(x)) for a polynomial f(x).
(b) In your notation, what is the irreducible polynomial over F5 of the element x + 1 of F25?
(c) Let G be the group of invertible 2 × 2 matrices with entries in F25. What is the order of G? How many conjugacy classes of G consist of elements of order 3? Find a representative for each of these conjugacy classes.
(d) Find a 3-Sylow subgroup of G. How many 3-Sylow subgroups does G have?
[4](a) Let G be a finite group acting on a finite set X. Prove Burnside's formula: The number of orbits of this action is
1/|G| Σg∈G|Xg|
where Xg denotes the set of elements in X that are fixed by g.
(b) Consider an unshaded n × n checkerboard, like the board shown for n = 5:
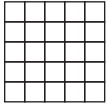
We would like to count the number of ways of placing two checkers on such a board, up to symmetry, where the board may be flipped or rotated. How would you formulate this problem as a group action? What is the group G? What is the set X? How many ways are there?
(c) Identify opposite sides of the board to form a torus, which may be flipped, rotated, or translated. Now what is the group G? How many ways can we place two checkers on this torus, up to symmetry?
[5](a) Describe the irreducible representations of the symmetric group S3, and their character table.
(b) How many irreducible representations does the symmetric group S4 have?
(c) How many irreducible representations does the alternating group A5 have?
[6](a) Let A be a square matrix that satisfies the matrix equation A2 - 5A + 6I = 0, where I is the identity matrix. What is the structure of the ring Z[A] generated by A over Z?
(b) Find a formula for An, as an element of Z[A].
[7](a) Define irreducible and prime for an integral domain. What is the relationship between euclidean, unique factorization, and principal ideal domains?
(b) List a few of the smallest irreducible elements of the integral domain
Z[√-2] = { a + b√-2 | a, b ∈ Z }
as measured by the norm N(a + b√-2) = a2 + 2b2. (In the complex numbers, this is length squared.)
(c) Is Z[√-2] a unique factorization domain?
(d) More generally, consider the integral domain
Z[√-c] = { a + b√-c | a, b ∈ Z }
where c is a positive integer. For which of these domains does the integer 6 factor uniquely into irreducibles?
[8] Let C[s, t] be the ring of polynomials on C2, and let C[w, x, y, z] be the ring of polynomials on C4. In other words, each element f of C[s, t] is a polynomial function f: C2 → C, and each element g of C[w, x, y, z] is a polynomial function g : C4 → C.
Consider the map α: C2 → C4 given by α(s, t) = (s3, s2t, st2, t3). The map α induces a ring homomorphism β: C[w, x, y, z] → C[s, t] given by the rule g |→ g o α. In other words, we restrict polynomials on C4 to the image of α, and pull back by α to obtain polynomials on C2.
(a) Describe the image of β as a subring R ⊂ C[s, t].
(b) Describe the kernel of β as an ideal I ⊂ C[w, x, y, z].
(c) An ideal P in a commutative ring R is prime if and only if the corresponding quotient ring R/P is an integral domain. Show that I is a prime ideal in C[w, x, y, z]. Find a strictly ascending chain I ⊂ J ⊂ K of prime ideals in C[w, x, y, z], where K is a maximal ideal.
[9] For any cubic polynomial f(x) = (x - α)(x - β)(x - γ), the discriminant D of f is defined to be
D = (α - β)2(α - γ)2(β - γ)2
(a) Derive a formula for D in terms of p and q, for polynomials of the form f(x) = x3 + px + q.
(b) Prove that the discriminant of an irreducible cubic polynomial f(x) in Q[x] is a square in Q if and only if the degree of its splitting field is 3.
(c) What is the degree of the splitting field of f(x) = x3 - 7x + 7?
[10](a) Prove the Eisenstein Criterion: If f(x) ∈ Z[x] and p is a prime, such that the leading coefficient of f(x) is not divisible by p, every other coefficient of f(x) is divisible by p, but the constant term is not divisible by p2, then f(x) is irreducible in Q[x].
(b) Show that x5 - 81x + 3 is irreducible in Q[x].
(c) Can x5 - 81x + 3 = 0 be solved by radicals?