Reference no: EM131108933
2009 Honors Examination in Geometry
[1] The map γ: R → R3 given by
γ(t) = (t, t2, t3)
defines a curve in R3. Compute its curvature and torsion.
[2](a) Give a parametrization of a torus S embedded in R3.
(b) Compute the Gauss map of S.
(c) Compute the Gaussian curvature at each point of S. What are the principal curvatures?
(d) Describe the Gauss map of the surface (x + y + z)2 - 2(x2 + x2 + z2) = 0.
[3](a) What aspects of hyperbolic geometry can you illustrate using the following Escher drawing, Circle Limit II?
(b) In combination, the uniformization theorem for surfaces and the Gauss-Bonnet theorem tells us that a closed surface of genus > 1 can be given a Riemannian metric of constant negative curvature. One way to form a genus 2 surface is by identifying sides of an octagon. Does the above tiling bear any relation to such a surface? Why or why not?
[4]A monomial ideal is an ideal in a polynomial ring k[x1, . . . , xn] generated by single terms. For example, I = (x2, xy, y2) is a monomial ideal in the polynomial ring C[x, y, z].
(a) Let I be a monomial ideal in the two variable polynomial ring k[x, y]. Show that I is finitely generated, without using the Hilbert basis theorem.
(b) Can you extend your proof to monomial ideals I ⊂ k[x, y, z]? (The general case is known as Dickson's lemma. It can be used to give an alternate proof of the Hilbert basis theorem.)
(c) Now suppose that I ⊂ k[x1, . . . , xn] is a radical monomial ideal. Give a bound on the number of monomials needed to generate I.
[5](a) State the Nullstellensatz.
(b) Give counterexamples over the real numbers R, the rational numbers Q, and the finite field with three elements F3 = Z/3Z.
(c) Algebraic geometers prefer to work over fields where the Nullstellensatz holds, and they prefer to work in projective space. Why?
[6](a) The Veronese surface is the image of the map α: P2 → P5 where
α(x, y, z) = (x2, xy, xz, y2, yz, z2)
Show that the Veronese surface is nonsingular.
(b) What is the tangent plane at each point α(x, y, z) of the Veronese surface?
(c) Each tangent plane corresponds to a point in the Grassmanian G(3, 6) of projective planes in P5.
Describe the map
α: P2 → G(3,6)
which takes each point (x, y, z) of P2 to the tangent plane of α(x, y, z).
[7](a) Describe the zero locus X ⊂ A2C of the equation xy2 - x4 = 0 in the affine plane over the complex numbers. Is X irreducible? Are the component(s) of X nonsingular? Describe the strict transform X~ of X after blowing up the origin. (X~ is "what happens to" X after blowing up.)
(b) Let Y be the curve defined by y2 - xd = 0 for d odd. What is the singular locus of Y? Can you use blowing up to transform Y into a nonsingular curve?
(c) The mathematician John Nash studied a variation on blowing up, associating each smooth point of a variety X with its tangent space, and taking the closure in hopes of smoothing out the singular locus. Can you make this idea work for y2 - xd = 0?
[8](a) The cubic equation (x + y)3 + xyz + z3 = 0 has four nontrivial integer solutions mod 2. What are they?
(b) This equation defines a cubic curve X ⊂ P2, and the above solutions are the four rational points of X over the finite field with two elements F2 = Z/2Z. Show that X is nonsingular at each of these points.
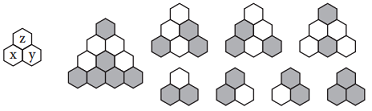
(c) The above illustration represents the cubic equation, its partial derivatives, and the solutions as diagrams shading the terms or entries that are nonzero. Can you devise rules for carrying out the calculations in (a) and (b) visually?
(d) The usual group law on elliptic curves can be used here to construct a group of order four. There are two possibilities: C2 × C2, or C4. Which group do we get? Can the other group also arise?
[9](a) Spherical distance is angle. Hyperbolic distance is sometimes described as imaginary angle. Certainly, the identity
cosh(x) = cos(ix)
suggests this. Can you reconcile any formulas from spherical and hyperbolic geometry using this idea?
(b) Work with the unit 2-sphere, and let
X = {(a2, b2, c2) | there exists a triangle with side lengths a, b, c}
Does X consist of an entire orthant? Is X unbounded? Give a geometric interpretation for X in a neighborhood of the origin.
(c) Now work with a hyperbolic plane having Gaussian curvature -1, and consider distances to be imaginary angles. Let
Y = {(-a2, -b2, -c2) | there exists a triangle with side lengths ai, bi, ci}
Does Y consist of an entire orthant? Is Y unbounded? Give a geometric interpretation for Y in a neighborhood of the origin.
(d) Algebraic geometers like to blow things up. (Hey, when you have a hammer, everything looks like a nail.) What can you say about the above picture after blowing up the origin?