Reference no: EM132584257

ENG762s2 Advanced Materials - University of Portsmouth

Task 1 Collagen fibrils are an important component of bone.

(a) Describe how collagen fibrils are formed from tropocollagen macromolecules.

(b) Explain where mineral forms within the collagen fibrils and why.

(c) Collagen fibrils in bone are typically 100 nm in diameter and have an elastic modulus of 1 GPa. The collagen fibrils are bound together by a non-collagenous protein with an elastic modulus of 50 MPa. For mature bone, the collagen fibrils are mineralized, with the mineral having an elastic modulus of 150 GPa and occupying a volume fraction of 50% within the collagen fibril. If the volume fraction of non-collagenous protein is 10%, what is the elastic modulus of the mineralized bone material. Make use of the rule-of-mixtures in your calculations.

(d) The result in c) is much larger than the experimental elastic modulus of a mineralized bone material. Give reasons as to why your answer is different to the experimental measurements.

(e) Suggest how organization of the collagen fibrils could be used to make bone a tough material.

Task 2

Micro-CT is an imaging technique that allows 3D visualisation and analysis of biological structures and engineering materials.

(a) Briefly schematise x-ray generation and physics.

(b) What is the SNR? Why is it important?

(c) What is BMD? Which technique is used to measure it and what are the main results?

(d) What is Computed Tomography? Briefly describe the process of projections acquisition and image reconstruction.

(e) How high-resolution micro-CT is currently used in the micromechanical characterisation of bone? Please comment on associated techniques used to quantify bone mechanical properties.

Task 3

Consider a cemented metallic femoral stem that is isotropic and is subjected to a multiaxial stress state as shown in the Fig. T3-1.

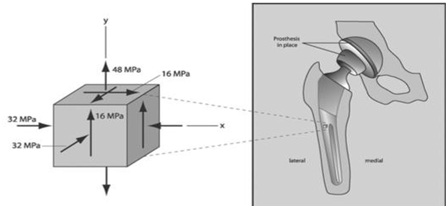
Fig. T3-1

These multiaxial stresses arise from several sources. From the joint contact force on the head, there is a net tensile bending stress (48MPa) on the lateral side of the stem, a shear force of 16MPa due to the load transmitted to the bone through the bone cement, and a compressive force in the transverse direction due to press fitting the implant in the bone (-32MPa). Assume that the alloy used in this device is made of an isotropic alloy that yields through a ductile shear mechanism. The orthopedic alloy has tensile yield strength of 900MPa. Calculate:

(a) The effective (von Mises) stress for this implant - how does this compare to the magnitude of the individual stress components? Determine whether this component is safely designed against yielding (calculate the factor of safety). Comment on your findings.

(b) Assume now that the stress state can be reduced to two dimensions, as shown in Fig. T3 -2, by neglecting the stresses acting in the z-direction. Determine the principal stresses and maximum shear stress for this 2D stress state. Calculate the effective stress for this implant. Which approach is more conservative?

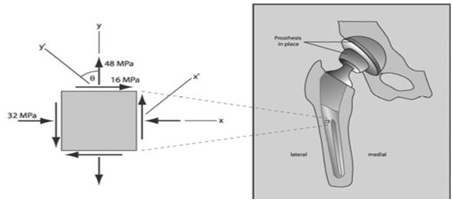
Fig. T3-2

Task 4

Many biological materials are composed of mixtures; for example, bone may be considered a mixture of collagen and mineral. Consider the elastic modulus of a mixture of two materials whose individual moduli are E1 and E2. The volume fractions of materials 1 and 2 are V1 and V2, respectively. It is known that the elastic modulus of the mixture has upper and lower limits given by mathematical models known as Voigt and Reuss models, respectively.

(a) What are the principal assumptions of such models?

Derive the following results for the modulus of the mixture:

(b) Voigt model, upper bound E = V₁E₁ + V₂ E₂

(c) Reuss model, lower bound E = E₁E₂ /(V₁E₂ + V₂ E₁)