Reference no: EM131641428

TRANSFORMATION:

From our experiences in previous units, we understand that congruence preserves size and shape. Any transformation involving congruence can be referred to as an isometry because distance is preserved. Also in previous units involving similarity and similarity theorems, we remember that similarity preserves shapes and angles but not size or distance. Transformations involving similarity, therefore, are not an isometry because distance is not preserved.

Objectives

- Find the image of points after a dilation
- Tell the difference between a contraction and an expansion
- Explore proportionality in triangle dilations

Question #1

Square EFGH underwent several transformations.

A. What is the correct value of d, being it is the value in which this square was transformed or dilated?

B. Explain how you calculated the value for d.

Question #2

The pentagon ABCDE is dilated to the image A'B'C'D'E' with the center of the dilation at the origin.

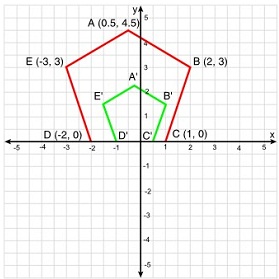
Select all true statements.

The scale factor of the dilation is 1/4

The line EA is parallel to the line E'A' because EA passes through the center of the dilation.

Since the line C'D' falls on the line CD, the scale factor is not applied on the line CD.

The scale factor of the dilation is 1/2

The line CD is not parallel to the line C'D' because CDpasses through the center of the dilation.

Question #3

The dilation D_O,2.5 is applied to triangle ABC below.

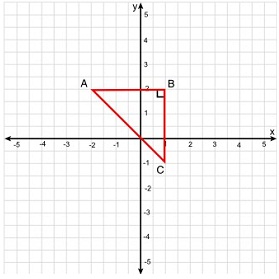
Use the dilation of triangle ABC and its image to prove that the dilation takes a line passing through the center of the dilation to the same line.

Question #4

Draw the dilation image A'B'C'D' of the trapezoid ABCD with the center of the dilation at the origin and the scale factor -2.

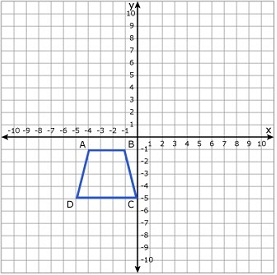
Question #5

Kyle claimed that the given quadrilaterals are similar because the ratio of their corresponding sides is equal.

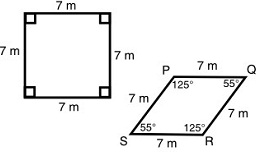
Is Kyle's claim incorrect or correct? In two or more complete sentences, justify your answer

Question #6

Allison claims that the ΔABQ is similar to ΔRPQ, given that AB and PR are parallel.

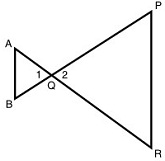
Which of Allison's claims supporting her argument are correct? Select all that apply.

∠1 = ∠2 because they are vertically opposite angles.

∠ABQ = ∠QPR because they are corresponding angles.

∠1 = ∠2 because they are alternate interior angles.

∠BAQ = ∠QRP because they are alternate interior angles.

ΔABQ and ΔRPQ are not similar by AA similarity.

Question #7

Use ΔJKL and ΔMPN to determine whether Don's claim is true or false.

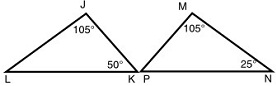
Which of the following should Don use to prove the triangles are similar?

SSS
SAS
AAS
AA

Question #8

Choose the correct description.

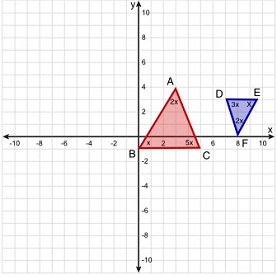
The angles of one triangle are in ratio x : 2x : 5x and the angles of another triangle are in the ratio x : 2x : 3x . The two triangles are ____ because at least one pair of corresponding angles are _____.

Question #9

Malaya is making a collage of her birthday party photos and she wants to add an 8 x 10 inch. photo. Since there is not enough space left on the collage, she must trim the photo. If the scale factor from the original to the trimmed photo is 5:4, the new dimensions of the photo are ____.

7 x 9 in
6.2 x 7.6
6.4 x 8 in
5.4 x 6.8

Question #10

What is the value of y?

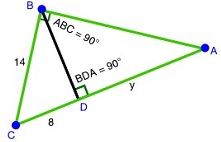
11.6 ft
12.5 ft
16.5 ft
17.5 ft

Question #11

What are the coordinates of M' after triangle MNO is reflected over the y-axis, and rotated 90 degrees clockwise with the origin as the center of rotation?

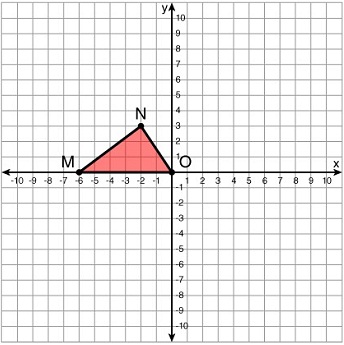
(6,0)
(0,6)
(-6,0)
(0,-6)

Question #12

Select all that apply.

The following graph shows an ellipse that suffered several transformations. Which of the following two sets of combinations of transformations could map ellipse 1 into ellipse 2? You may choose more than one correct answer.

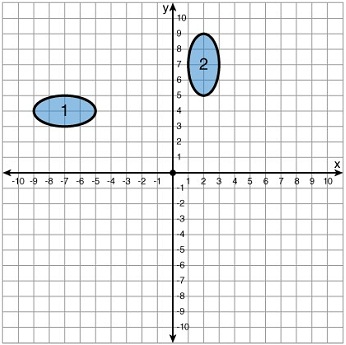
Translation 3 units up and 7 units to the right
Reflection along the y-axis and translation 3 units to the left
Rotation of 90° clockwise by the origin O, and translation 2 units to the left

Reflection along y = -x, and translation 6 units to the right

Question #13

A dilation centered at the origin is applied to the line y = 3x + 5.

What is true about the image of the line?

It is the same line.
It is another line parallel to y = 3x + 5 The image is not a line.
The question cannot be answered without knowing the scale factor.

Question #14

A triangle has vertices at O(0, 0), A(1, 0), and B(0, 1). A dilation centered at (1, 0) is applied to the triangle.

____ of the sides lie on the same line as their respective images.

Dilations in a Triangle

Question #15

If you wish to show that two triangles are similar, which statement(s) is correct? You may choose more than one
correct answer.

It is enough to show that two pairs of corresponding angles are congruent.
It is enough to show that two pairs of corresponding sides are in the same ratio.
It is enough to show that all three pairs of corresponding sides are in the same ratio.
It is not enough to have information about only sides or only angles.

Question #16

Show Answer

a dilation is applied to a triangle, then the image must be _____.

a larger or smaller triangle. a congruent triangle.
a triangle that is rotated about a given point.
a triangle that is flipped over a line of symmetry.

Question #17

A dilation is applied to a triangle such that the sides of the image are 1.5 times the length of their corresponding sides in the original triangle.

Then the angles of the image must be 1.5 times the size of the corresponding angles in the original triangle.

Then the angles of the image must be two-thirds the size of the corresponding angles in the original triangle.

Then the angles of the image must be 3 times the size of the corresponding angles in the original triangle.

Then the angles of the image must be congruent to the corresponding angles in the original triangle.

Question #18

In the diagram below, side XY is parallel to side X'Y'.

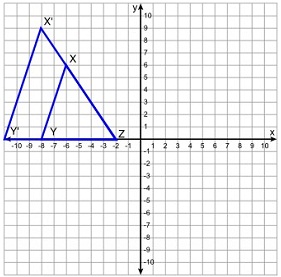
There is a dilation centered at ___  with a scale factor of ____ which will transform triangle XYZ into triangle X'Y'Z.

Question #19

Two right triangles are shown below.

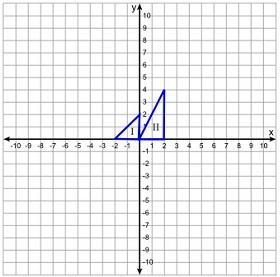
Which statement is true?

There is a dilation centered at the origin with scale factor 2 transforming triangle I into triangle II.

There is a dilation centered at (-2, 0) with scale factor 2 transforming triangle I into triangle II.

There is a dilation centered at a point off of the x-axis transforming triangle I into triangle II.

There is no dilation transforming triangle I into triangle II.

Question #20

Given ΔRST and ΔR'S'T'.

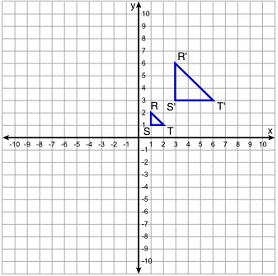
a. Describe a dilation (center and scale factor) that transforms triangle RST into triangle R'S'T' or explain why it cannot be done.
b. In either case, use complete sentences to describe the relationship that exists between the corresponding sides and angles

Question #21

Draw a triangle with vertices A(0, 4), B(2, -2), and C(-2, -2). Apply a dilation centered at the origin with scale factor 1/2 to this triangle and draw the resulting triangle, ΔA'B'C'.

In complete sentences, describe the following:
a. The relationship between corresponding sides in terms of their lengths.
b. The relationship between corresponding sides in terms of their orientations.
c. The relationship between corresponding angles in terms of their measures.