Reference no: EM131503313

Report

The term report is like a "small research project" to allow you to apply the physical principles and techniques taught in class to solve some real photonic device problems. Here you will be asked to solve the same problem in several different approaches, to develop physical insight about photonic devices.

To enhance your physical understanding of the problem, you are NOT supposed to use COMSOL Physics or any EM solver to numerically solve the problem. You need to mathematically formulate the problem step by step, and then solve the problem analytically (if possible) or numerically with the assistance of Matlab.

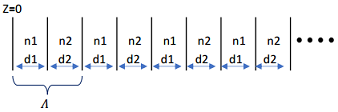
1. We have a 1-D periodic structure made of alternating layers with their index of refraction being n₁ and n₂ (n₁ = 2.7 and n₂ = 3.5).

(a) Derive the time-independent wave equation as:

(b) Find the eigen values and eigen functions using the Bloch theorem.

The above time-independent wave equation with periodic index is similar to the 1D Schrodinger equation. Let us try to solve the problem in a similar approach as we solve the Schrodinger equation in a Kronig-Penny model (i.e. having a square wave-like periodic potential).

Write the general solution of the E-field in region 1 (with index n1) and region 2 (with index n2) as:

E(z) = Ae^jβ_1z + BAe^-jβ_1z           0 ≤ z ≤ d₁                        β₁ = k_on₁

E(z) = Ce^jβ_2z + D^e-jβ_2z            d₁ ≤ z ≤ d₁ + d₂ = Λ         β₂ = k_on₂

Use the boundary conditions at z = d₁, we obtain two equations due to the continuity of tangential E and tangential H at the interface z = d₁.

Because the solution can be written as a "Bloch wave" as the electron wave-function in a periodic potential, the Bloch theorem in semiconductor physics tells us

E(z + Λ) = E(z)e^jβΛ

This gives us two additional boundary conditions at the position z = d₁ + d₂ = Λ.

Write down the 4 boundary conditions in the following matrix form:

Remember ω = k_oc. Therefore, by solving the equation: det[V] = 0, we obtain ω as a function of β. This is the "photonic band structure" for this 1D photonic crystal.

Use Matlab program to solve the above problem and plot ω(β). Also plot the ω(β) diagram in the "reduced band structure" in the "1^st Brillouin zone (i.e. limit the β value to the "photonic first Brillouin zone: - (π/Λ) ≤ β ≤ (π/Λ)).

Identify the "photonic bandgaps" in your band structure.

(c) Find the coefficients A, B, C, D (i.e. B, C, D in terms of A, which can be an arbitrary number). Show that E(z) is indeed a Bloch wave in the following form:

E(z) = Uβ(z)^jβz where U_β(z) = U_β(z + NΛ) is a periodic function.

2. For the same 1D photonic crystal in (1), you will analyze the problem in a different approach (s-matrix) as described below:

(a) Consider the layer 0 ≤ z ≤ d₁. Treat the layer as a "two-port system" with incident and reflected waves at the input and output ports.

For a single layer 0 ≤ z ≤ d₁, we can assume A(0), B(d₁) to be incident waves at ?? = 0 and d₁.

Write the S-matrix as

where β₁ = k_on₁, r₂₁ = n₁-n₂/n₁+n₂ is the field-reflectivity for a plane wave incident from an n₂ layer and reflected at the n₂/n₁ interface.

From the above relation, reorganize the terms to prove that

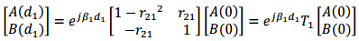
Note that now the transfer matrix can be cascaded.

(b) Following the similar approach in (a), find the transfer matrix T₂ in the following expression:

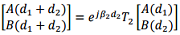
(c) Assuming the photonic crystal has a total of N period, find the transfer matrix, T, of the entire crystal:

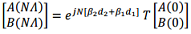
(d) Calculate the reflectivity of the N-period photonics crystal (Bragg reflector). Also show the expression for the special case when n₁d₁/λ_o = n₂λ₂/λ_o = ¼.

r = B(0)/A(0)|_{B(NΛ) = 0}

(e) Compare your results in (d) with the result from the coupled-mode theory discussed in class. Under what conditions the two results become close to each other (note that the coupled-mode theory results are approximations and here the analysis is "exact"). Can you find the expression of the "coupling coefficient" by comparing the two results?

(f) The E-field at each interface between the nth interface of n1and n2 layers can be written as:

E(nΛ) = A(nΛ) + B(nΛ)

E(nΛ + d₁) = A(nΛ + d₁) + B(nΛ + d₁)   n = 0,1,2 ... ..

Find the E-field at these positions: E(nΛ) and E(nΛ + d₁).

Find E(z) for all z positions and plot |E(z)|². The results should be the same as the result in problem 1(c).

3. Problems 1, 2 talk about 1D photonic crystal, now let us extend the analysis to 2D photonic crystals. The index of refraction is represented as

N(x, z) = n_o + [∑_mn_me^iGmx][∑_nn_ne^iGnz]            G = 2π/Λ

(a) Show that the time-independent wave equation can be approximately written as

(b) Assume E(x, z) = X(x)Z(z). Show that the above wave equation can be written as

X'' + k_o²n_o∑_mn_me^iGmx + β_x² = 0

Z'' + k_o²n_o ∑_nn_ne^iGnz + [k_o²n_o² - β_x²] = 0

β_x is the projection of the wave vector in the x-axis.

(c) We will leave the problem to this stage. Hope that by now you can fully appreciate the similarity between the problem of semiconductor and photonic crystal and the subtle differences as well.

If you like and have time, you can go on and actually solve a 2D photonic crystal band structure.