Reference no: EM131110576

2007 Honors Examination in Probability

1. Let Y have a Gamma (α, β) distribution with density given by

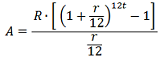
where α and β are positive. Let µ (µ > 0) be the mean of Y and σ² be the variance of Y. Note that ₀∫^∞f_Y (y|α, β)dy = 1.

(a) Show that the moment generating function (MGF) of Y is M_Y(t) = (1 - βt)^-α.

(b) Derive the mean and variance of Y from the MGF.

(c) What is the distribution of Z = cY, where c is a positive number?

(d) What is the probability density function (pdf) of W = 1/Y?

2. Let Y₁, Y₂, ... be independent and identically distributed random variables with Poisson (λ) distributions. Let Y_n^- = 1/n _i=1∑ⁿ Y_i.

(a) Given an upper bound on the probability that Y₁ is greater than 2.5 λ.

(b) What are the mean and variance of Y_n^-? Explain why.

(c) Prove the Weak Law of Large Numbers (WLLN) as applied to Y_n^-.

(d) State a Central Limit Theorem (CLT) result as applied to Y_n^-.

3. Let Y_i, i = 1, . . . , n be independent and identically distributed Gamma (1,β) = Exponential (β) random variables.

(a) What is the cumulative distribution function (CDF) for Y₁? Use the CDF to express the probability that Y₁ is between 1.5 and 3.5.

Suppose β has prior distribution specified as an Inverse-Gamma (1, ν) distribution. The probability density function of β is

f(β) = 1/β²e^-1/(βν)

for β, ν > 0.

(b) What is joint density of the data and β?

(c) What is the posterior distribution of β given observations y_i, i = 1, . . . , n?

4. A basketball player attemps to throw ("shoot") the basket ball into the basket ("the goal") while standing a certain distance away from the basket ("behind the free throw line") n = 40 times. Assume the trials are independent of one another and each time there is a probability p = 0.7 of success.

(a) What is the distribution of the number of failures ("misses")? What is the expected number of the number of misses?

(b) What is the distribution of the number of tries until the first miss? What are the expected number of tries until the first miss?

Let X_i(i = 0, . . . , n) have 3 possible values: -1, 0, or 1. Let X₀ = 0. If the player makes a basket on trial i, then X_i remains at 1 if X_i-1 was 1 and X_i = X_i-1+1 otherwise. If the player misses the basket on trial i, then X_i remains at -1 if X_i-1 was -1 and X_i = X_i-1-1 otherwise.

(c) Set up the matrix of transition probabilities, P, for the Markov chain (X_i, i = 0, . . . , n). Use the matrix of transition probabilities to compute the probability that X₉ = 1 given that X₆ = -1.

(d) Is the Markov chain any of the following: absorbing, ergodic, or regular? Briefly explain.

(e) What is the limiting matrix, W, of the Markov chain?

(f) What are the expected return times for the states in the Markov chain?

5. Suppose there are C people at a party and each person has a coat in a pile in the bedroom. Unfortunately, the coats fall on the floor and the power goes out. Assume each person can identify her or his coat based on feel. Each person enters the bedroom, picks a coat, and leaves with it if it is her or his coat. Otherwise, after everyone has picked out a coat, the person puts the coat back in the pile. Subsequent rounds of selection are similar but involve only the remaining people and their unclaimed coats. Let N be the number of rounds until all people get their coats. Let M_n be the number of people at round n. Obviously M₀ = C and M_N = 0. Define the number of people who find their coats during round n + 1 as X_n+1, where Mn+1 = M_n - Xn+1, n ≥ 0.

(a) Show that E(X_n+1) = 1, n ≥ 0. Hint: show first that E(X₁) = 1.

(b) Show that E(M_n+1 + n + 1|M₀, . . . , M_n) = M_{n + n}.

(c) Is S_n = M_n + n a martingale (a fair game)? Why or why not?

(d) Argue that P(N < ∞) = 1.

(e) Here is a theorem: Let S_n be a martingale and N a stopping time for S_n. Then E(S_N) = E(S₀) if |S_n| ≤ K for all n, where K is a real positive finite constant, and P(N < ∞) = 1. Apply this theorem to determine E(N).

6. A coin is tossed until tails appears. On each flip the probability of heads is p (0 < p < 1) and of tails is q = 1 - p. Flips are independent of one another. Let N be the number of heads.

(a) What is the probability that N = k, for k a nonnegative integer?

(b) Simplify the probability generating function for N. The probability generating function for random variable N is G_N(s) = E(s^N) for some value s.

(c) For each head a value for a random variable with a Poisson(λ) distribution is generated. The random variable for the i^th head is X_i, λ > 0, and all the Xi's are independent of one another. What is the probability generating function of X_i? Call this function G_X.

(d) For a given value of N, what is the probability generating function of Z = X₁ + · · · + X_N? Call this function G_Z|N.

(e) Show that G_Z(s) = G_N(G_X(s)), where G_Z, G_N, and G_X are the probability generating functions for random variables Z, N, and Xi for any i.

(f) Use the result of the previous part to produce the probability generating function of Z. You may use the result even if you have not proved it.

(g) Use the result of the previous part to determine E(Z). If you do not have the probability generating function of Z, then use a probability generating function to find one of the following: E(N), E(Z|N), or E(X_i).