Reference no: EM132186674

Calculus of complex and vectors, and transforms

Outline: This coursework requires you to:

1. Use complex analysis to solve problems in calculus.

2. Determine the gradient, divergence and curl of scalar and vector quantities as appropriate, state the theorems of Gauss, Green and Stokes and apply them in a selection of case studies from physics and engineering.

3. Analyse periodic phenomena into corresponding Fourier series, using both analytic and numerical techniques.

4. Know the basic properties of the complex Fourier transform, including the Fourier Inversion Theorem, and be able to calculate direct and inverse Fourier transforms, applying these results to convolution integral equations; and be able to use the Laplace transform method to solve linear ordinary differential equations and convolution type integral equations.

Task 1. Vector Calculus

a) If Φ = xy³z², and F = xz^i - y²j^ + 2x²yk^, find:

i. ∇Φ
ii. ∇·F
iii. ∇×F
iv. div(ΦF)
v. curl(ΦF)

b) If F = (x, -y), compute ∫_C F·dr for each curve C defined below:

i. C is the curve along y = e^x, from x = 1 to x = 3.
ii. C is part of the circle of radius 3 in the first quadrant from (3,0) to (0,3)
iii. C is the part of the curve x = cos(y) from y = 2Π to y = 0

c) Verify Green's theorem for F = (xy, x²y³) on a closed curve that is a triangle with vertices (0,0), (1,0), (1,2) with negative orientation.

Task 2. Complex Analysis

a) Consider the following complex functions. Decide which of these are
• Continuous.
• Differentiable/analytic

If certain complex values of z give rise to different properties, you should identify these clearly. Give your own calculations to illustrate or prove your conclusions in each case.

i. f(z) = z-1/z-1
ii. g(z) = 1/4z²-1
iii. h(z) = cosh(z)

b) Let

f(z) = 1/z²

Work out the integral of f(x + iy) around the rectangle between the lines x = -1, x=1, y= -2 and y= 1 by

i. Evaluating the integral along each side of the rectangle.
ii. Cauchy's integral formula.

Task 3. Fourier Series

Consider a half-wave rectifier output current, I amperes, defined by

          A sinω₀t    0 < t < T₀/2

l(t) =                                             l(t + T₀) = l(t)

              0         T₀/2 < t < T₀

where A = 3, ω₀ = 2Π/T₀ = 3.

a) Derive the Fourier series for the function l(t).

b) Use a suitable computer algebra software to confirm your result. Produce a single plot showing the Fourier series representation of l(t) over [0, T₀], using the first 5 terms, 10 terms and the first 30 terms of the series. Comment on your plots.

Note: when using computer algebra, you should include screen dumps of actual commands used and plots obtained in your submission.

Task 4. Fourier Transform

Consider the function:

f(t) =  0 |t| > 10
cost  -10 ≤ t ≤ 10

a) Use the Fourier's integral theorem to derive the Fourier transform of f(t).

b) Use the Fourier transforms of the top-hat and sine/cosine functions, and properties of the Fourier transform to confirm your result.

c) Use suitable computer algebra software to confirm your result. Produce two graphs showing the amplitude and phase spectra, |F(ω)| and Φ(ω), respectively, over -3 ≤ ω ≤ 3, if F{f(t)} = F(ω). Discuss how these plots relate to the Fourier transforms of the top-hat and cosine functions.

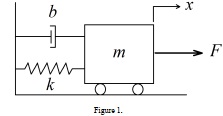
Task 5. Laplace Transform and differential equations

Consider the mass-spring-damper system shown in Figure 1. At time t = 0, the system is at position x = 0, with velocity x′ = 0. We state the system can be modelled with the following differential equation:

mx''(t) + bx'(t) + kx(t) = F(t)

a) Use Laplace transform to find x(t) for i. F(t) = δ(t),
i. F(t) = c(t)

b) Use a suitable computer software to produce plots of x(t). Comment on your plots.