Reference no: EM13967844

1. Give an example of a dictionary for which the current basic feasible solution is optimal and yet the coefficients of the non-basic variables in the z row are not all negative.

2. Take your final dictionary to your Quiz 2 after corrections if any are required (if you haven't picked it up remember to do so) and verify the revised simplex formulas. Namely identify B, A_N, c_B, c_N, x_B, x_N and then compute B^-1 and the z row using z = c_B^T B^-1b + (c_N^T - c_B^TB^-1A_N )x_N and then the remaining equations as x_B = B^-1b - B^-1A_Nx_N.

If you move the non basics to the left of the equations, the matrix B^-1 can be read off as the coefficients of slack variables. Of course you don't have to change the dictionary and can do this directly but then the columns are either the negative of the coefficients of a slack variable if it is non-basic variable (recall x_B = B^-1b - B^-1A_nx_N ) and an appropriate column of a single 1 if the slack variable is a basic variable.

3. Theorem 5.5 is taken from page 65-66 of V. Chvatal's book on Linear Programming. Consider the LP:

maximize ∑ⁿ_j=1 cjxj

subject to ∑ⁿ_j=1 a_ijx_j ≤ b_i (i = 1, 2, . . . m)

x_j ≥ 0 (j = 1, 2, . . . , n)

Theorem 5.5. If (5.24) has at least one non-degenerate basic feasible optimal solution, then there is a positive s with the property: If |t_i| ≤ s for all i = 1, 2, . . . , m, then the problem

maximize ∑ⁿ_j=1 c_jx_j

subject to ∑ⁿ_j=1 a_ijx_j ≤ b_i + t_i (i = 1, 2, . . . m) (5.25)

x_j ≥ 0 (j = 1, 2, . . . , n)

has an optimal solution and its optimal value equals

z∗ + ∑^m_i=1 y_i^∗t_i

with z∗ standing for the optimal value of (5.24) and with y₁^∗, y₂^∗, . . . , y_m^∗ standing for the optimal solution of its dual.

Now consider the following LP

max 12x₁ +20x₂ +18x₃
       4x₁ +6x₂ +8x₃ ≤ 600
       x₁ +(7=2)x₂ +2x₃ ≤ 300  x₁, x₂, x₃ ≥ 0
       2x₁ +4x₂ +3x₃ ≤ 550

The final dictionary is:

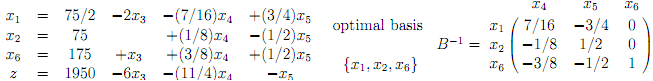
Does Theorem 5.5 apply here?

For what value of s (choose the largest possible for this particular data!) is the theorem true? In this case I will offer you an hint about computing ∈. Hint: If you have been given an inequality 3t₁ - 5t₂ ≤ 5 which must hold for any choices t₁, t₂ satisfying -s ≤ t₁ ≤ s and -s ≤ t₂ ≤ s, then we deduce that s ≤ 5/8.

4. Consider our two phase method in the case that the LP is infeasible. We begin with the primal LP

max    z
      Ax ≤ b .
       x ≥ 0

We introduce an artificial variable x₀ and obtain the new LP (in Phase 1)

max -x₀
          x₀

[-1| A] x ≤ b,

x₀ ≥ 0, x ≥ 0,

where (-1) is the vector of -1's and we use [-1 | A] to denote the matrix obtained from A by adding one more column (of all -1's) on the left. We assume the maximum value of the objective function in the new LP is strictly negative. (In general this would depend on whether the original LP is infeasible; we assume the original LP is infeasible)

a) Derive the dual of the new LP. Verify that an optimal dual solution will verify (certify?) that the inequalities above do not have any feasible solution. Namely explain why

y^T A ≥ 0^T , y ≥ 0 , b.y < 0 will show that there is no feasible solution to the original LP.

b) Verify that for an optimal dual solution (the magic coefficients!) y = (y₁, y₂, . . . , y_m)T we have y₁ + y₂ + ......+ y_m = 1. (You may note that in assignment 1, the sum was 1/2 + 1/3 + 1/6 = 1).

a) Extend the standard theorem of the alternative as follows.

Let A be an m × n matrix and b be an m × 1 vector. Let u be an n × 1 vector (of upper bounds). Prove that either:

i) there exists an x with Ax ≤ b, x ≤ u

or

ii) there exists vectors y, z with A^Ty + z = 0, y, z ≥ 0, b.y + u.z < 0 but not both.

You may use the dual introduced in Assignment 1, question 5 to handle free variables.

b) Use a) to show that the following system of equalities with bounded variables given below has no solution. You can guess y, z for the given data:

-x₁ -x₂ ≤ -6

-x₁ +x₂ ≤ -8

x₁ -2x₂ ≤ 3

x₁ ≤ 4

x₂ ≤ 2