Reference no: EM13952066

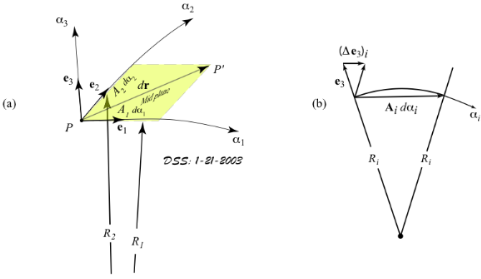
Figure 1. (a) Curvilinear coordinates at the mid-plane showing unit vectors. (b) Geometry of change in unit normal vector.

The reference orthogonal curvilinear coordinate system with corresponding unit vectors is shown in Figure 1. It is clear that the unit vectors are functions of the in-plane coordinates, α₁, and α₂. In order to develop a metric for distance, and subsequently displacement and strain, in terms of the curvilinear coordinates, it is necessary to determine the functional relationships between the unit vectors and their derivatives, and the curvilinear coordinates, α₁, and α₂. Towards that end, we note the following:

dr = ∂r/∂α₁dα₁ + ∂r/∂α₂dα₂        (1)

Letting,

r_α1 = ∂r/∂α₁                           (2)

and

r_α2 = ∂r/∂α₂                           (3)

we have

dr = r_α1.dα₁ + r_α1.dα₂            (4)

From Figure 1 b, where to first-order approximation the arclength defined by Aidα_i may be approximated by its chord, and where the change in the unit normal in the i^th-direction is given by

(Δe₃)_i = (∂e₃/∂α_i)dα_i               (5)

Applying a similar-triangle argument, we can determine the unit normal derivative relations

∂e₃/∂α₁ = (A₁/R₁)e_{1                    (6)}

and similarly,

∂e₃/∂α₂ = (A₂/R₂)e_{2                    (7)}

where A₁ = |r_α1|                     (8)

and A₂ = |r_α2|                        (9)

are the Lame parameters. Given the above, we can now define the curvilinear unit vectors in terms of known quantities as follows:

e₁ = r_α1/A₁                              (10)

e₂ = r_α2/A₂                              (11)

and

e₃ = e₁ x e₂                              (12)

Noting that we may write

r_α1 = A₁e₁                                 (13)

and

r_α2 = A₂e₂                                 (14)

we define the following very useful identity

∂r_α1/∂r_α2 = ∂r_α2/∂r_α1                 (15)

Which, of course, implies

∂(A₁e₁)/∂α₂ = ∂(A₂e₂)/∂α₁                 (16)

Equations (15), and (16) are valid since for analytic functions, the order of differentiation does not matter. Likewise, we have

∂²(e₃)/∂α₂∂α₁ = ∂²(e₃)/∂α₁∂α₂                 (17)

Given the above development,

Question: 1. Derive expressions for the derivatives of the unit vectors, e₁ and e₂ with respect to α₁, and α₂ in terms of A₁, A₂, R₁, and R₂ to add to those already developed for e₃. You make use of the orthogonality of the unit vectors, and identities like the following

e₂.∂e₁/∂α₁ = ∂/∂α₁(e₁.e₂) - ∂e₂/∂α₁.e₁ = -∂e₂/∂α₁.e₁   (18)

in this derivation. Note that by orthogonality, the first term on the rhs of (18) vanishes. Equation (18) yields the projection of the given derivative in the e₂ direction - i.e. the magnitude of its e₂ component.

Question: 2. Derive Codazzi's conditions given by:

∂/∂α₁(A₂/R₂) = 1/R₁.∂A₂/∂α₁       (19)

and

∂/∂α₂(A₁/R₁) = 1/R₂.∂A₁/∂α₁       (20)

You will find the derivative relations that you derived and the identity given by Equation (17) useful in this derivation!

Question: 3. Derive Gauss's condition given by

∂/∂α₁(1/A₁.∂A₂/∂α₁) + ∂/∂α₂(1/A₂.∂A₁/∂α₂) + A₁A₂/R₁R₂ = 0       (21)

You will find Equation (16) useful here.