Demonstrate that the following fas are equivalent

Assignment Help Basic Computer Science

Reference no: EM13972561

For each of the following pairs of regular languages, find a regular expression and a Finite Automata (FA) that each define L1 intersection L2.

L1 L2

1. (f + e)e (f + e)* e(f + e)*

2. (d + c)*d c(d + c)*

3. All string of even length = (cc + cd + dc + dd)* (c + d)*d

4. Even-length strings c(c + d)*(c + d)*c

5. (c + dc)*(d + ^) (d + c)*dd(d + c)*

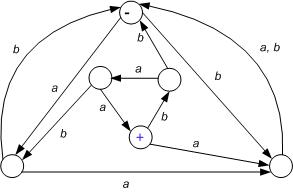
6. Demonstrate that the following FAs are equivalent (as in Chapter 11), or determine if they are not. Then,

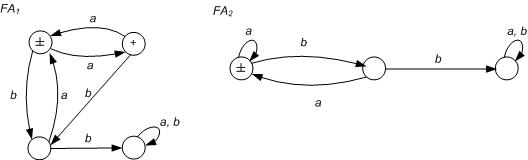
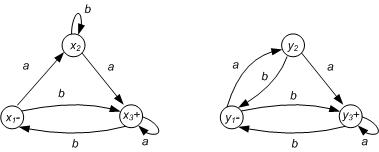
7. Demonstrate that the following FAs are equivalent (as in Cohen Chapter 11), or determine if they are not.

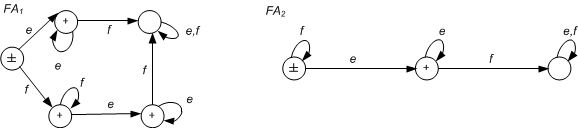
8. Demonstrate that the following FAs are equivalent (as in Cohen Chpt 11), or determine if they are not.

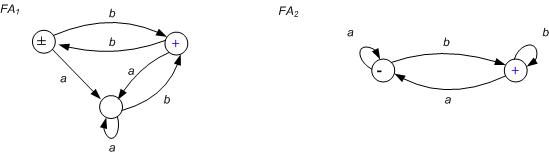
9. Using the method of intersection each machine with the complement of the other, show that the following machines do not accept the same language.

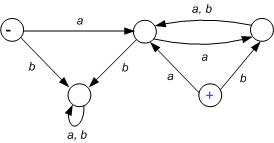
10. By using blue paint, determine if the following FA accepts any words:

11. Again using blue paint, determine if the following FA accepts any words:

Reference no: EM13972561

Questions Cloud

What are the prices of the two bonds if the relevant market : What are the prices of the two bonds if the relevant market interest rate decreases to 7.6%? What are the prices of the two bonds if the relevant market interest rate increases to 12.9%?

What techniques do the authors use in their portrayals : What techniques do these authors use in their portrayals of these issues, and how effectively does each one make his/her point?

Net cash inflows and outflows into a single payment : Each of the following factors is sometimes a constraint on the free movement of funds internationally. Why would a government impose such a constraint? How might the management of a multinational argue that such a constraint is not in the best intere..

Create a graph of the hanging weight m1g vs. acceleration : Using the information you obtained in parts (a) and (b), predict what the value of the acceleration would be if the value of the hanging mass were increased tom1 = 0.35 kg.

Demonstrate that the following fas are equivalent : For each of the following pairs of regular languages, find a regular expression and a Finite Automata (FA) that each define L1 intersection L2.

Reasons behind the establishment of nonsmoking areas : Discuss the reasons behind the establishment of nonsmoking areas in public facilities and restaurants. In California, there are now bans on the sale and consumption of shark's fin and goose liver (foie gras) placed on the basis of animal protectio..

What is the current share price : Bayou Okra Farms just paid a dividend of $2.65 on its stock. The growth rate in dividends is expected to be a constant 4.5% per year indefinitely. Investors require a return of 15% for the first 3 years, a return of 13% for the next 3 years and a ret..

What is the amount of bond premium amortization : What is the amount of bond premium amortization for the June 30, 2005, adjusting entry?

Experiencing rapid growth-projected dividend for coming year : Momsen Corp. is experiencing rapid growth. Dividends are expected to grow at 30% per year during the next 3 years, 20% the following year and then 6% a year indefinitely after that. The required return on this stock is 10%, and the stock currently se..

User Account

All Pages