Reference no: EM133373791

Principles of Data Science

Module - Principles of Data Science

Learning Outcome 1: Demonstrate systematic knowledge and critical understanding in topics in linear algebra, probability and statistical models, relevant to data science.

Task: This Individual Coursework involves investigating the different properties and operations involving vectors, matrices and probability, including Markov chains and Eigenfaces. You are encouraged to explore the topic, use your initiative, and show some originality, within the time available. Make sure you read each task through carefully, and answer all parts of each task.

Task 1: Markov Chains

Example: Flowers. Consider a particular variety of flower which can take one of three colours: red, white and pink. Suppose after each year, 40% of red flowers remain red but 60% of red flowers mutate to pink. For pink flowers, 30% mutate to red, 50% remain as pink, and 20% mutate to white. For white flowers, 90% remain as white and 10% mutate to pink. We can capture these probabilities in a transition matrix P where the columns correspond to red, pink and white flowers in the current year and the rows correspond to red, pink and white flowers in the next year.
      [0.4 0.3  0 ]
P =  [0.6 0.5 0.1]
       [0 0.2 0.9]
If a certain garden initially has 80 of this variety of red flowers and 20 of this variety of white flowers then after one year:
     80     32
P [ 0 ] = [50]
     20     18
so we would expect to see 32 red, 50 pink and 18 white flowers in the garden. If we look at the garden after 5 years:
          80            80      20.88
PPPPP [ 0 ] = P5 [ 0 ] = [37.08]
          20           20       42.04
so we would expect to see approximately 21 red, 37 pink and 42 white flowers in the garden. This is an example of a system called a "Markov chain". The next state of the system depends only on its present state and does not depend on the earlier history of the system.

Assessment: Mice in a maze. Consider the closed maze shown below containing seven rooms (labelled 0 to 6) with doorways connecting the rooms. A number of mice are placed in the maze and the mice then move randomly from room to room. Each time step, a mouse either stays in the same room (with probability 0.6) or leaves the room it is in by choosing at random (equally likely) one of the doors out of the room.

 

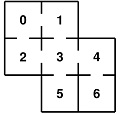
(1) Construct a 7 × 7 transition matrix P (as a numpy array) to model the mice moving around the maze as a Markov chain.

(2) Suppose that 50 mice are placed in Room 0 and 90 mice are placed in Room 1. All other rooms are initially empty. Use numpy to calculate how many mice we would expect to see in each room at the end of each time step for each of the next 30 time steps. Use Python to plot your results on a line graph showing one line for each room, together with a legend. Briefly comment on what you observe. You might find numpy.linalg.matrix_power() helpful.

(3) Use numpy to find the eigenvectors of the transition matrix P from part (1), and explain how one of these eigenvectors is related to the number of mice we would expect to see in each room in the "long-run steady state". Also, for each room j, find the expected number of time steps for a particular mouse initially located in room j to first return to room j. Hint: if Pj is the probability that the particular mouse is in room j in the "long-run steady state" then the expected first return time is given by 1/Pj .

(4) Suppose the mouse population is in the "long run steady state" from part (3) when a large piece of poisoned cheese is placed in Room 6 so that any mouse that enters that room instantly dies.

(a) Modify the transition matrix P from part (1) and estimate the number of time steps until 80% of the mice have died.
(b) The expected number of time steps needed for a mouse starting from room ?? to reach room k for the first time can be calculated using matrix operations and is denoted ????k . For a particular destination room k, let ?? be the transition matrix P from part (4)(a) but with row k and column k both deleted, and let ?? be the 6 × 6 identity matrix. The sum of each column of the matrix (?? - ??)-1 gives the values ????k . Use this method to find the expected number of time steps needed for a mouse to die, for each of the possible rooms in the maze that the mouse could start from. Briefly comment on what you observe.

Task 2. Eigenfaces

The Olivetti Faces dataset consists of 400 images of human faces. Five examples are given below.

Each image is 64 pixels wide by 64 pixels high. However, the Python code below assembles the 400 images as columns of the matrix Xall. Each image is greyscale (not colour) and all pixel values are between 0 and 1. The matrix Xsub is the last 300 columns of the matrix Xall.

The only Python libraries you may use in this task are numpy and matplotlib, except that you may use sklearn only to load the dataset as in the Python code below.

import sklearn.datasets
faces = sklearn.datasets.fetch_olivetti_faces()
Xall = faces.data.T print(Xall.shape) print(Xall.min(), Xall.max()) Xsub = Xall[:,100:]

(1) Use numpy to find the mean of each row of Xsub and reshape as a 4096 × 1 vector (call this xbar). Adapt the Python code below to visualise this "mean face" and compare it to the image stored in the column of Xall corresponding to the last two digits of your Student ID.

plt.imshow(**something**, cmap=plt.cm.gray, vmin=0, vmax=1)

(2) Use numpy.cov() to calculate the covariance matrix of Xsub, giving a 4096 × 4096 matrix (call this matrix ??). Then use numpy.linalg.eigh() to find the eigenvalues (??) and eigenvectors (columns of the matrix P) of ??. Use the Python code below to reverse the entries in ?? and the columns of P. Let ?? be the diagonal matrix consisting of the elements of ?? along its diagonal. Use numpy to confirm that P is an orthogonal matrix and that ?? = P??P??.

Make sure you use numpy.linalg.eigh() not numpy.linalg.eig() for this part.

V = V[::-1]
P = P[:,::-1]

(3) In the following Python code, we apply P?? (as a matrix transformation) to the faces in Xsub, where xbar is the "mean face" (a 4096 × 1 vector) from part (1).

Ysub = P.T@(Xsub-xbar)

(a) The eigenvectors of ?? (i.e. the columns of P) are called "eigenfaces" (Turk and Pentland, 1991). Visualise the eigenfaces corresponding to the largest 10 eigenvalues. Comment on what you discover. You will need to remove vmin and vmax from the plt.imshow() example given above.

(b) Show (by example) that if y is any one column of Ysub then P@y+xbar perfectly recreates the corresponding column of Xsub. This shows that each "face" in Xsub is a "linear combination" of eigenfaces plus the "mean face".

(c) Although P is a 4096 × 4096 matrix, generally only those eigenfaces corresponding to the largest eigenvalues of ?? are "useful". If there are k such eigenvalues (with k ≥ 2), let Xpartial be the matrix formed from matrix multiplication of the first k columns of P and the first k rows of Ysub, and adding xbar. Investigate how well Xpartial approximates Xsub for different values of k by using the numpy.linalg.norm() function applied to Xpartial minus Xsub (this provides a measure for "goodness of fit"). Build an appropriate line graph as part of your investigation.