Reference no: EM131304799
Mathematical Modelling and Analysis Assignment - Framework Design
A framework of pin jointed members has to be designed to support an emergency sluice gate in a tidal barrage wall. The gate is 1.0m high, 1.0m wide and its top edge is located 1.0m below the maximum allowable water level. The gate is to be attached to the framework on its upper and lower edges via pin joints. The frame is anchored to the gate opening mechanism via a pinned support and a rolling support as shown in Fig.1.
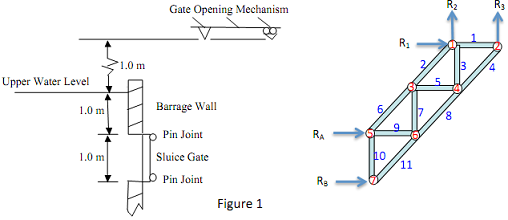
A framework has been designed as shown in Figure 1, which consists of 11 individual members as numbered. The lengths of members 1, 3, 5, 7, 9 and 10 are all 1 meter, and all other members are √2 meters long.
1) RA and RB are the reaction forces at the pin joints of sluice gate due to the water pressure (P = ρgh). Calculate both RA and RB by applying equilibrium condition for the gate, and define RA and RB in Matlab.
2) In order to calculate 11 unknown member forces (N1 to N11) and 3 unknown reaction forces R1, R2 and R3, the Method of Joints needs to be used, and this provides an analytical way of calculating all forces within a statically determinate structure. Each of 7 joints or nodes is analysed in turn, taking the sum of the horizontal and vertical forces acting on the node. These will both be equal to zero because neither the node nor the framework is accelerating. When each node has been considered, a set of equations will result which include all member forces and reactions on the framework. The equations for each node will be in term of the forces present in the members joining to that node. In a statically determinate structure, the number of unknowns must be equal to the number of equations. To solve these equations, convert them to a matrix format AX=B, where A is an 14 by 14 coefficient matrix, X = [N1 N2 N3 ... N11 R1 R2 R3]T is the unknown vector, and B = [0 0 0 0 0 0 0 0 RA 0 0 0 RB 0]T is the known vector containing external reaction forces RA and RB. Using a single PDF to record the entire procedure of how to derive the linear equation system AX=B by using the Method of Joints. Using Graph function and Equation tool in MS Word to plot each free body diagrams and define equation system.
3) Define vector B and the stiffness matrix A for the system in Matlab and compute the unknown vector X using matrix methods using Matlab.
4) Use commented text (denoted by the prefix %) in your Matlab script to show all individual member forces and 3 reaction forces R1, R2 and R3.
5) Briefly describe the problem, and discuss / verify your results (e.g. apply static equilibrium of forces to verify 3 reaction forces) using commented text in Matlab.