Reference no: EM133354173

Question 1: Consider the linear system of equations:

x₁ + 2x₂ + x₃ = -α
x₁ + 3x₂ + 2x₃ = 1
3x₁ + 7x₂ + α2x₃ = 3 - α

Find conditions on α ∈ R such that the system has no solutions, a unique solution, and infinitely many solutions. In the latter two cases, find the solution set in R3×1. (Note. Your solutions may be in terms of α.)

Question 2. Define the linear transformation T : P₂(R) → R^3×1 as

 

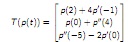
where p'(t) is the derivative of p(t) and p"(t) is the second derivative of p(t). As an example, T (3 + 2t + t²) = (11, 5, -2)^T. Additionally, define

 

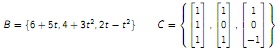
as well as the standard bases

 

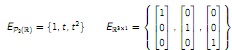
(Note. Throughout your solutions, you may use without proof the fact that EP₂(R) is a basis for P₂(R) and E_R3×1 and C are bases for R^3×1.)

(a) Prove that B is a basis for P₂(R).
(b) Find R(T ) and rank(T ).
(c) Find N(T ) and null(T ).
(d) Is T injective, surjective, both, or neither? Explain briefly.
(e) Find [T ]E_R3×1 ,EP_2(R). (f) Find [T]_C,B.

Question 3. Let A, B ∈ C^n×n such that AB = 0. Prove or disprove each of the following statements:
(a) Either A = 0 or B = 0 (or both).
(b) BA = 0. (c) (BA)² = 0.
(d) If tr(A) = -4, then B = 0.
(e) If det(A) = -4, then B = 0.
To disprove a statement, provide a counterexample for n = 2. Include a brief explanation confirming that your chosen matrices form a counterexample.

Question 4. Let B ∈ C^n×n be a specific fixed matrix. Define V_B to be the set of matrices in C^n×n that commute with B, that is
V_B = {A ∈ C^n×n : AB = BA}.

Prove that V_B is a subspace of the complex vector space C^n×n (with the usual matrix addition and scalar multiplication).