Reference no: EM13733602
Waiting Line Problem 1
During the evening busy period, passengers of United Airlines at the Medford International Airport arrive at a rate of 71 per hour and an agent can serve 26 passengers per hour. The check-in queue system the airline follows is illustrated below:
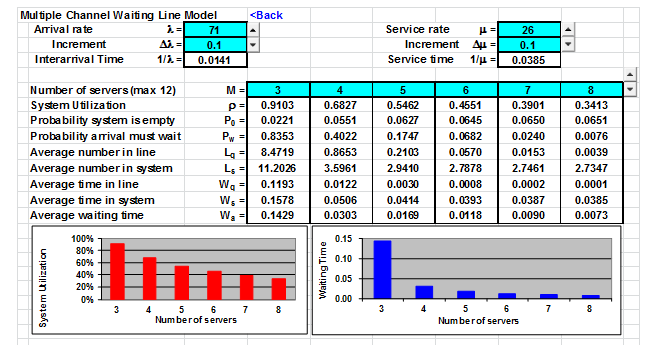
1. The channels in this queuing problem are the:
a. Only the United Airlines passengers at the Medford Airport
b. All the airline passengers at the Medford Airport
c. Agents at the counters of all the airlines at the Medford Airport
d. Agents at the counters of United Airlines at the Medford Airport
e. None of the above
2. The customers in this queuing problem are the:
a. Only the United Airlines passengers at the Medford Airport
b. All the airline passengers at the Medford Airport
c. Agents at the counters of all the airlines at the Medford Airport
d. Agents at the counters of United Airlines at the Medford Airport
e. None of the above
3. In terms of the waiting line model that is appropriate for this situation, the calling population (or population source) could be best described as:
a. Finite
b. Infinite
c. Neither of the above
4. The arrival and service patterns, respectively, for this queuing situation could be best described as:
a. Constant arrival rate, constant service rate
b. Constant arrival rate, variable service rate
c. Variable arrival rate, constant service rate
d. Variable arrival rate, variable service rate
e. None of the above
5. The appropriate queuing model for this problem is:
a. Single channel, exponential service time
b. Single channel, constant service time
c. Multiple channel, exponential service time
d. Multiple priority service, exponential service time
e. None of the above
6. On average, how many United Airlines passengerscan be served per hour during the busy evening hours if there are 3 agents on duty? ____________________
7. What is the average time customers spend in line waiting for service if3 agents are on duty during this busy evening period? Express your answer in minutes. _______________
8. When 3 agents are on duty during this busy evening period, what is the likelihood that an arriving UAL passenger will have to wait for service upon arriving at the counter? Express your answer as a percent. __________
9. When 3 agents are on duty during this busy evening period, on average, how many UAL passengers are in the system (in line plus being served)? _________
10. If UAL management wants to limit the length of time passengers have to be in the system - in line plus service time - to under 3 minutes, how many agents should UAL have during this busy time)? _______
Waiting Line Problem 2
The manager of a warehouse must decide on the number of loading docks to request for a new facility in order to minimize the sum of dock costs and driver-truck costs.
The manager has learned that each driver-truck combination represents a cost of $600 per day and that each dock plus loading crew represents a cost of $1,000 per day (or per 8 hours). The arrival and service rates in the output below are per day.
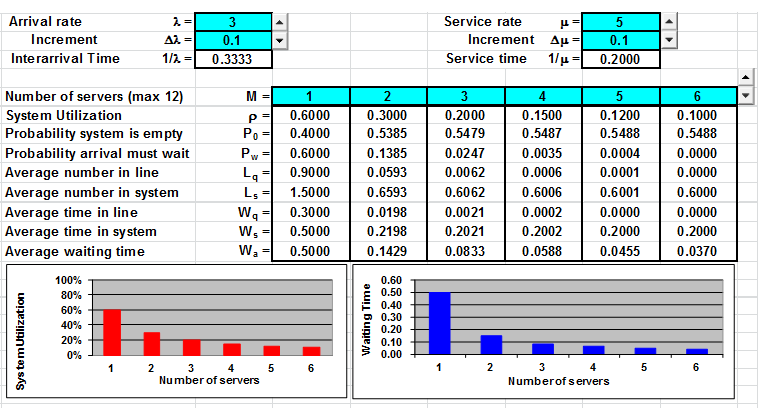
11. This queuing problem involves which of the following waiting line models?
a. Single channel, exponential service time
b. Multiple channel, exponential service time
c. Finite population queuing model
d. None of the above
12. Which of the following is/are true for this queuing problem?
a. The population source is infinite
b. The arrival pattern of customers (trucks needing to be unloaded) is variable
c. The service pattern is variable
d. The dock(s) is(are) the channel(s)
e. All of the above are true for this queuing problem.
13. If ONE loading dock is built on the new facility, what is the average waiting time (in HOURS) for trucks to unload their cargo? _________________
14. If only ONE loading dock is built on the new facility, what is the expected time a truck will be in the system (waiting plus loading time)? _________________
15. If the goal of the manager is to limit the average waiting time for the trucks to unload to LESS THAN ONE HOUR, how many loading docks should the new facility have? _________________
16. If the goal of the manager is to minimize the total cost of waiting (dock and crew cost plus driver and truck cost), how many loading docks should be built? _______________
17. When the number of loading docks is increased (e.g. from 1 to 2, or 2 to 3, etc.), which of the following statements would NOT be true?
a. The total cost of loading crew per day will increase
b. The total cost associated with trucks (including the driver)waiting in line will decrease
c. The average number of trucks in line will decrease
d. The probability that an arriving truck will have to wait for unloading will decrease
e. Utilization level of the loading docks will increase
Q.C. Problem 1
Specifications for a critical part for a DVD player state that the part should weigh between 22 and 26 ounces. The process that produces the parts yields a mean of 24.5 ounces and a standard deviation of 0.85 ounce. The distribution of the weights of the part is normal.
18. What proportion of parts will meet the weight specs? _____________
19. If in a production month 1,000,000 of this part are produced, how many are expected to be discarded because of non-compliance to specs? (round up to the nearest unit) ____________
20. Each part costs $100 to produce. If in a production month 1,000,000 of this part are produced, what is the expected cost of the discarded parts for the month? _______________
21. If the production process for this part is redesigned, and the variation inherent in the process is improved, this redesign will result in:
A. Less discarded parts
B. More discarded parts
C. No change in expected number of discarded parts
Q.C. Problem 2
|
Five data entry operators work of Data Processing department each day for 20 days the number of defective records in a sample of 250 records typed by these operators has been noted, as follows:
|
|
|
|
Sample No.
|
No. Defective
|
Sample No.
|
No. Defective
|
|
|
1
|
7
|
|
11
|
12
|
|
|
|
2
|
5
|
|
12
|
5
|
|
|
|
3
|
10
|
|
13
|
20
|
|
|
|
4
|
10
|
|
14
|
4
|
|
|
|
5
|
11
|
|
15
|
11
|
|
|
|
6
|
8
|
|
16
|
8
|
|
|
|
7
|
6
|
|
17
|
12
|
|
|
|
8
|
9
|
|
18
|
4
|
|
|
|
9
|
6
|
|
19
|
6
|
|
|
|
10
|
13
|
|
20
|
25
|
|
|
22. What is the size of each sample (i.e. what is the sample size)? ____________
23. How many samples does this QC problem have? ____________
24. The appropriate chart for this problem is:
A. Mean chart
B. Range chart
C. P-chart
D. C-chart
E. None of the above
25. What is the proportion of defective records for the 20th sample? _______
26. What is the overall proportion of defective records (average sample proportion)? __________
27. Assume that the company will institute a re-training program for its data entry operators if the control chart indicates an out-of-control process (e.g. when it is concluded that a higher proportion of defective records than normal has occurred). Given this, what will be the cost or consequence associated with a Type II error?
A. There will be more dissatisfied customers (as a result or more data entry errors) than what the company would be willing to accept
B. The expense associated with an unneeded training program
28. What is the correct interpretation of the Type I error in this situation?
A. The company would conclude that the proportion of defective records IS within the acceptable range when it really is NOT.
B. The company would conclude that the proportion of defective recordsis NOT within the acceptable range when it really IS.
29. Based on the control chart you created, was the process in control during the observation period?
a. Yes
b. No
IM Problem 1
|
Michigan State Figurine Inc. (MSF) sells crystal figurines to Spartan fans. MSF buys the figurines from a manufacturer at $10 per unit. They send orders electronically to the manufacturer, costing $20 per order and they experience a lead time of 8 days for each order to arrive from the manufacturer. Their inventory carrying cost is 20%. The average daily demand of the figurines is 20 units per day with a standard deviation of 3 units. They are open for business 250 days a year.
|
|
| |
| |
|
30. The company is open 250 days per year. What is the annual demand for the figurines? _____
31. If the current ordering policy of MSF is to order twice a year, how large is the order size (Q) for this order policy? _____
32. How much is MSF's carrying (or holding) cost per unit per year if they order twice a year? ____________
33. If MSForders at the EOQ, how many units should be ordered each time? ___________
34. At the EOQ, what is MSF's total cost (holding plus ordering) per year? _____________
35. Refer to the graph in question #36 below. Which of the following represents the EOQ you computed in #34?
a. A
b. B
c. C
d. D
e. E
f. F
g. None of the above
36. Refer to the graph below. Which of the following represents the average daily demand for the figurines?
a. A
a. B
b. C
c. D
d. E
e. F
f. None of the above
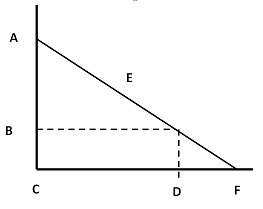
37. What is the safety stock level for thefigurines at 90 percent service level (round up)? _____________
38. Over how many working days will each order (EOQ) last (round up)? ___________
IM Problem 2
|
Bryson Carpet Mills produces a variety of different carpets. Changing from production of one carpet to another involves a setup cot of $1,000. One particular carpet costs $5 per yard to produce. Annual demand for this style is 120,000 yards. BCM produces carpet 300 days per year. The production process is most efficient when 4,000 yards per day are produced. Inventory carrying cost is estimated at 20% annually.
|
|
|
|
39. Given the information above, on a cost basis, what is the optimum run size for thecarpets? ____
40. How many batches (round up to a whole number)of the carpets will be run each year? __________
41. At EPQ, what will be the maximum inventory for each run cycle (batch)?______________
42. On average, how manyyards of carpets will the factory have in its inventory? ____________
43. For each production run, over how many days (hint: time between T1 and T2) will the factory be producing carpets (round up to a full day)? ___________
44. How many days (round up to a full day) will the maximum inventory last? _____________
Use this graph to answer questions 45 to 50
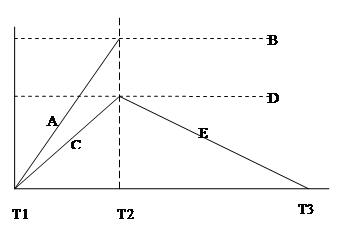
45. What does the slope of line C represent? (Refer to the graph above)
a. Maximum Inventory = 14,697 yards
b. Rate of production per unit time = 4,000 yards
c. Rate of increase in inventory per unit time = 3,600 units
d. Usage rate of accumulated inventory per unit time = 400 yards
e. None of the above
46. What does the dashed line B represent? (Refer to the graph above)
a. Maximum Inventory = 14,697 yards
b. Rate of production per unit time = 4,000 yards
c. Rate of increase in inventory per unit time = 3,600 units
d. Usage rate of accumulated inventory per unit time = 400 yards
e. None of the above
47. What does the dashed line D represent? (Refer to the graph above)
a. Maximum Inventory = 14,697 yards
b. Rate of production per unit time = 4,000 yards
c. Rate of increase in inventory per unit time = 3,600 units
d. Usage rate of accumulated inventory per unit time = 400 yards
e. None of the above
48. The period between T1 and T2 represents which of the following? (Refer to the graph above)
a. Production period for the item
b. Time at which the accumulated inventory of the item is being used
c. Time at which inventory for the item is being accumulated
d. (a) and (b)
e. (a) and (c)
49. The period between T2 and T3 represents which of the following? (Refer to the graph above)
a. Production period for the item
b. Time at which the accumulated inventory of the item is being used
c. Time at which inventory for the item is being accumulated
d. (a) and (b)
e. (b) and (c)
50. Which of the following represents the rate at which the inventory of the carpet is increasing in each production day? (Refer to the graph above)
a. Slope of A
b. Slope of B
c. Slope of C
d. Slope of D
e. Slope of E