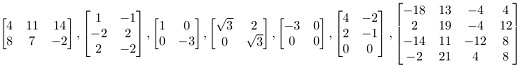Reference no: EM132590085

Assignment - Linear Algebra

Q1. Define echelon form and row reduced echelon form of a matrix.

Q2. Find out (i) the echelon form and row reduced echelon form, (ii) pivot element, pivot column, (iii) the solution of the following system equation.

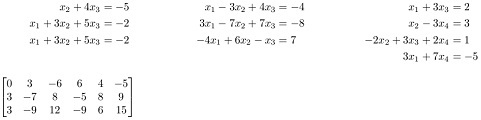
Q3. Theorem to be noted: Each Matrix is equivalent to one and only one reduced echelon matrix.

Q4. Define span of a set of vector.

Q5. Let 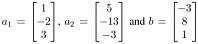. Then span [a₁, a₂] is a plane through origin in R³. Is b in that plane?

Q6. Let 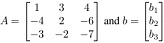, Is the equation Ax = b consistent for all possible b₁, b₂, b₃?

Q7. Let 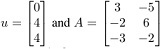, Is the u in plane R³ spanned by the columns of A? Why or why not? Explain with geometric figure.

Q8. Let 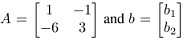. Show that the equation Ax=b does not have solution for all possible b, and describe the set of all b for which Ax = b does not have solution.

Q9. Determine if the following homogeneous system has a nontrivial solution. Then describe the solution set.

3x₁ + 5x₂ - 4x₃ = 0

-3x₁ - 2x₂ + 4x₃ = 0

6x₁ + x₂ - 8x₃ = 0

Q10. Write the working formulas of matrix algebra (Hints: see matrix cookbook).

Q11. Find the LU factorization of

Q12. Define a vector spaces and subspaces of a vector space.

Q13. Give examples of a vector space, a subspace and not a subspace.

Q14. Define column space and null space of a matrix.

Q15. Let 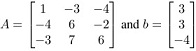, Determine whether b is in the column space of A.

Q16. Define basis of a subspace.

Q17. Find the basis of the column space and null space of the following matrix. What is the dimension of column space and null space?

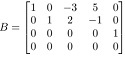
Q18. What is the row rank, column rank and dimension of null space?

Q19. Find the basis of null and column space of the following matrix.

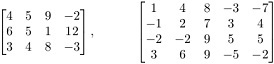
Q20. Theorem to be noted: If a matrix A has n columns, then rank(A) + dim(Null(A)) = n.

Q21. Find a basis for the subspace spanned by the given vector. What is the dimension of the subspace?

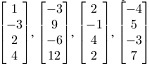
Q22. Find a spanning set for the null space of the matrix.

Q23. Find a matrix A such that W = Col(A).

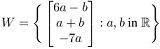
Q24. Theorem to be noted: The Pivot columns of A form a basis for Col A.

Q25. Find bases for the row space, the column space, and the null space of the matrix.

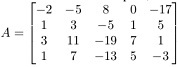
Q26. Diagonalize the following matrices, if possible (find an invertible matrix P and a diagonal matrix D such that A = PDP^-1).

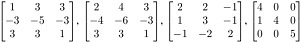
Q27. Theorem to be noted: An n x n matrix with n distinct eigenvalues is diagonalizable.

Q28. det(A - λI) = λ² - 3λ + 2 = (λ - 2)(λ - 1). The eigenvalues are 2 and 1, and the corresponding eigenvector are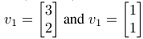. Find A⁸ using Aⁿ = PDⁿP^-1, Where P = [v₁v₂] and D = .

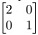Q29. Compute u.v and v.u when 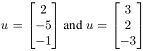. Also determine length of the above two vectors and unit vectors of u and v.

Q30. Prove that the two vectors to be Perpendicular if u.v = 0.

Q31. Theorem to be noted: Let A be an m x n matrix. The ortogonal complement of the row space of A is the null-space of A, and the orthogonal complement of the column space of A is the null-space of A^T i.e. (RowA)⊥ = Nul A and (ColA)⊥ = Null A^T.

Q32. Let 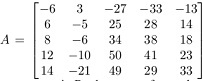. Construct a matrix N whose columns from a basis for Null A, and construct a matrix R whose rows from a basis for Row A. Now verify the above theorem.

Q33. Show that {u₁, u₂, u₃} is an orthogonal set, where .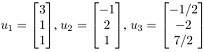

Q34. Theorem to be noted: If S= {u₁, . . . , u_p} is an orthogonal set of non-zero vectors in Rⁿ, the S is linearly independent and hence is a basis for the subspace spanned by S.

Q35. Theorem to be noted: An orthogonal basis for a subspace W of Rⁿ. For each y in W, the weights in linear combination y = c₁u₁ + . . . + c_pu_p, where c_j = (y.u_j)/(u_j.u_j) (j= 1, . . . , p).

Q36. Let 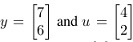. Find the orthogonal projection y onto u. Then write y as the sum of two orthogonal vectors, one is span {u} and an one orthogonal to u.

Q37. Show that {v₁, v₂, v₃} is an orthonormal basis of R³, where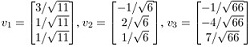

Q38. Determine which sets of vectors are orthonormal. If a set is only orthogonal, normalize the vector to produce orthonormal set.

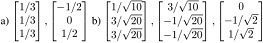
Q39. Theorem to be noted: Let W be a subspace of Rⁿ. Then each y in Rⁿ can be written uniquely in the form y = y^{^} + z, where, y^{^} is in W and z is W^⊥. In fact, if {u₁, . . . , u_p} is any orthogonal basis of W, then y^{^}= ((y.u₁)/(u₁.u₁))u₁ + . . . + ((y.u_p)/(u_p.u_p))u_p, and z = y - y^{^}.

Q40. Let 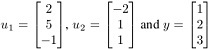. Observe that {u₁, u₂} is an orthogonal basis for W = Spanu₁,u₂. Write y as the sum of a vector in W and a vector orthogonal to W.

Q41. The distance from a point y in Rⁿ to a subspace W is defined as distance from y to the nearest point in W. Find the distance from y to W = Span{u₁, u₂}, where .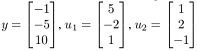

Q42. Theorem to be noted: If {u₁, . . . , u₂} is an orthonormal basis for a subspace W of Rⁿ, then proj_Wy = (y.u₁)u₁+ (y.u₂)u₂+ . . . + (y.u_p)u_p. If U = [u₁u₂. . . u_p], then proj_Wy = UU^Ty for all y in Rⁿ.

Q43. Verify the theorem with the problem 41.

Q44. What is GRAM-SCHMIDT process?

Q45. Let 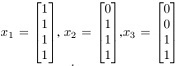. Then {x₁, x₂, x₃} is clearly linearly independent and thus is a basis for a subspace W of R⁴. Construct an orthogonal basis for W.

Q46. Theorem to be noted: (The Gram-Schmidt Process) Given a basis {x₁, . . . , x_p} for a subspace W of Rⁿ, define

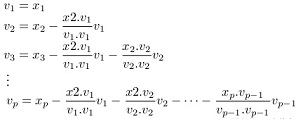
Then {v₁, . . . , v_p} is an ortogonal basis for W. In addition Span {v₁, . . . , v_k} = Span {x₁, . . . , x_k} for 1 ≤ k ≤ p.

Q47. Theorem to be noted: (The QR Factorization) If A is a m x n matrix with linearly independent columns, the A can be factored as A = QR, where Q is an m x n matrix whose columns form an orthonormal basis for Col A and R is an n x n upper triangular invertible matrix with positive entries on its diagonal.

Q48. Find an orthonormal basis for the column space of each matrix.

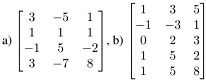
Q49. Suppose A = QR, where Q is m x n and R is n x n. show that if the columns of A are linearly independent, the R must be invertible.

Q50. Suppose A = QR, where R is an invertible matrix. Show with an example that A and Q have the same column space.

Q51. Theorem to be noted: (The Single Value Decomposition) Let A be an m x n matrix with rank r. Then there exists an m x n matrix ∑ for which the diagonal entries in D are the first r singular values of A, σ₁ ≥ σ₂ ≥ . . . σ_r > 0, there exists an m x m orthogonal matrix U and an n x n orthogonal matrix V such that A = U∑V^T.

Q52. Construct a singular value decomposition of following matrices.