Reference no: EM13916762

ASSIGNMENT 1

Question 1:

Recall that a monoid consists of a set, M, with distinguished element e and a binary operation

: M × M → M, (x, y) → x.y

such that for all x, y, z ∈ X

(i) (x.y).z = x.(y.z)

(ii) e.x = x = x.e

Let A be an object of the category C.

Show that C(A, A), the set of all morphisms f : A → A, forms a monoid.

Question 2:

Let ob(C) and ob(D^r) both be the set of all open subsets of Rⁿ for all counting numbers n. For the open subset X of Rⁿ and the open subset Y of R^m with m, n counting numbers, put

C(X, Y ) = {f : X → Y | f is continuous}
D_r(X, Y ) = {f : X → Y | f is r times differentiable}
Show that C and Dr are small categories.

Question 3.

Let A be an object of the category C.

For the object X and morphism f : X → Y of C, define

(i) F^AX = C(X, A)
(ii) F^Af = f* : C(Y, A) → C(X, A), g → gof

Show that FA, which is also denoted C(, A), is a contravariant functor

F^A : C → Set

Let a : A → B be a morphism in C.

For each object X of C, define

α_X : C(X, A) → C(X, B), h -→ a o h

Show that

α : FA ⇒ FB, X → αX

is a natural transformation.

Question 4.

Let F be a field.

Put ob(C) = N, the set of all natural numbers. For natural numbers m, n, put

C(n, m) = M(m × n; F)

the set of all m × n matrices with coefficients in the field F. Define composition of morphisms to be matrix multiplication. Show that C is a skeletal category.

Show that F-Vec, whose objects are all finitely generated vector spaces over F, and whose morphisms are F-linear transformations, is a category.

For each finitely generated F-vector space, V, choose a basis BV . Define F : F-Vec → C as follows.

(i) For the finitely generated F-vector space, V, FV = dimF V the dimension of V as vector space over F.

(ii) For the F-linear transformation T : V → W , FT = AT , the matrix of T with respect to the bases BV for V and BW for W.

Show that F is a functor.

Question 5.

Let Ring₁ be the category whose objects are unital rings ("rings with 1") and whose morphisms are unital ring homomorphisms, where if R and S are unital rings, then the function f : R → S is a unital ring homomrphism if and only if for all x, y ∈ R,

(i) f (x + y) = f (x) + f (y)
(ii) f (xy) = f (x)f (y)
(iii) f (1_R) = 1_S

We regard Z and Q as unital rings.

Then the inclusion function ι : Z → Q is a morphism in Ring₁.

Let R be a unital ring and take morphisms (that is, homomorphisms of unital rings) f, g : Q → R. Show that f = g if and only if f o ι = g o ι.

Show that Ring1(Q, Z) = ∅, that is, there are no morphisms Q → Z.

ASSIGNMENT 2

Question 1.

Let o and * be group operations on the set G.

Suppose that e ∈ G is the neutral element for both o and * and that for all a, b, c.d ∈ G
(a o b) * (c o d) = (a * c) o (b * d)
Prove for all x, y ∈ G
(i) x * y = x o y
(ii) y * x = x * y

Question 2.

Let i_x^y: X → Y, x → x be the inclusion function of the subset X of Y into Y. Show that for all sets A, B

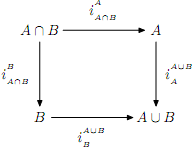
is both a push-out diagram and a pull-back diagram in Set, the category of sets and functions between them.

Question 3.

Given sets, X, Y , put

X ∪ Y := (X × {Y}  ∪ {X} × Y
and define
in_X : X -→ X ∪ Y, x → (x, Y )
in_Y : X -→ X ∪ Y, y → (X, y)
Show that (X ∪ Y ; in_X, in_Y ) is the coproduct of X and Y in Set.

Question 4.

Given V, W vector spaces over the field F, put

V ⊕ W := {(v, w) | v ∈ V, w ∈ W}

For v, x ∈ V, w, y ∈ W and λ ∈ F, define

(v, w) + (x, y) := (v + x, w + y)

λ.(v, w) := (λv, λw)

Take linear transformations

prV : V ⊕ W → V, (v, w) → v

prW : V ⊕ W → W, (v, w) → w

in_V : V → V ⊕ W, v → (v, 0_W)

in_V : W → V ⊕ W, w → (0_V , w)

Show that .V ⊕ W ; pr_V , pr_W. is the product of V and W in Vec_F, the category of vector spaces over F and F-linear transformations.

Show that .V ⊕ W ; in_V , in_W. is the co-product of V and W in Vec_F.

Question 5.

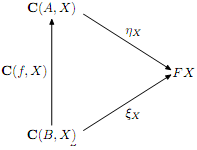
Let F : C → Set be a representable functor.

Prove that the object representing F is uniquely determined up to unique isomorphism.

That is, given natural isomorphisms η : C(A, ) ⇒ F , ξ : C(B, ) ⇒ F , there is a unique isomorphism f : A → B such that for each object X, we have a commutative diagram