CVE80004 Advanced Concrete Design Assignment

Reference no: EM132495669

CVE80004 Advanced Concrete Design Assignment - Swinburne University of Technology, Australia

A 150 mm thick reinforced concrete slab is supported on all 4 sides as denoted in the diagram.

The nominal moment capacities are

Φmu_x⁺	10 kNm/m
Φmu_x^-	8 kNm/m
Φmu_y⁺	7 kNm/m
Φmu_y^-	6 kNm/m

All reinforcing is Grade N.

Permanent load (DL) and imposed load (LL) factors are as given in Lecture 1.

Self-weight is the only permanent load.

Reinforced concrete nominal density is as given in Lecture 1.

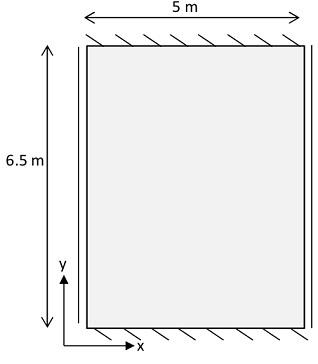
1) If the slab is supported on all 4 sides as denoted in the diagram, use yield-line theory to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support.

2) If the slab is simply supported on all 4 sides (instead of supported as denoted in the diagram), use yield-line theory to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support.

3) If the slab is supported on all 4 sides as denoted in the diagram, use published coefficients for rectangular slabs with standard support conditions and uniform loading in AS 3600 to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support.

4) If the slab is simply supported on all 4 sides (instead of supported as denoted in the diagram), use the strip method to calculate the nominal value of uniformly distributed imposed load (LL) that the slab can support. For the strip method distribute the total load 71% spanning in the x direction and 29% spanning in the y direction, and calculate the moments in the strips using elastic analysis

Show all working (including differentiation for the yield-line method).

Reference no: EM132495669

Questions Cloud

Calculate the amount of interest that should be recognized : AAA needs to prepare end-of-year adjustment for interest on the note. Calculate the amount of interest that should be recognized

Find what is the equipments after-tax net salvage value : Find What is the equipment's after-tax net salvage value? Enter your answer in dollars. For example, an answer of $1.2 million should be entered as 1,200,000.

Find what is the projects operating cash flow : Find The company faces a 25% tax rate. What is the project's operating cash flow for the first year (t = 1)? Enter your answer in dollars.

Calculate the two projects net present value : Calculate the two projects' NPVs, assuming a cost of capital of 10%. Do not round intermediate calculations. Round your answers to the nearest cent

CVE80004 Advanced Concrete Design Assignment : CVE80004 Advanced Concrete Design Assignment Help and Solution - Swinburne University of Technology, Australia. Calculate nominal value of imposed load

Find what is the project npv : Find What is the project's NPV? (Hint: Begin by constructing a time line.) Do not round intermediate calculations. Round your answer to the nearest cent.

Find the net present value : Find the weighted average cost of capital (WACC). (Do not round intermediate calculations, round final answer to two decimals, i.e. 123.45)

What rate of return is the franchiser using : What rate of return is the franchiser using and what method did Heaven Pizza use to calculate it? What rate of return is Joe using and what method did he use?

Calculate the amount that should have appeared : Calculate the amount that should have appeared in the estimated Warranty Provision account at the end of 2018. Assume the balance in the Warranty Provision

User Account

All Pages