Reference no: EM133168946

CSCI 4650 Numerical Analysis - University of Colorado

Assignment 1:

Question 1. What is the smallest number of multiplications and additions needed to evaluate P (x) = 4x⁶ + 2x² + 2x + 6 at x = 1/3.

Question 2. What are the most number of multiplications and additions needed to evaluate a degree n polynomial, a₀ + a₁x + a₂x² + .... + + a_nxⁿ using nested multiplication.

Question 3. Convert 110 .110 from binary to decimal.

Question 4. Covert 7 .2 from decimal to binary.

Question 5. Create a function in Python which takes a positive integer as an input and outputs its binary repre- sentation.

Question 6. A long double floating point number has 1 bit for a sign, 15 bits for an exponent, and 64 bits for the mantissa. What is ∈_mach? Explain your reasoning.

Question 7. Consider the function

f (x) = 1 - (1 - x)³/x

(a) Give an alternate form of f (x) which avoids the issue of subtraction by nearly equal numbers when x is close to 0.

(b) Create a table of the values that Python outputs for f (x) and your alternate form from (a) for x = 10-k for k = 0, 1, 2, . . . , 10.

Question 8. Consider the function

f (x) = ln(x)

(a) Find the Taylor polynomial of degree 4 around the point x = 1.

(b) Use your answer from (a) to estimate ln(1.01) and use the remainder theorem to say how large your error could be between the estimate and true value. Finally use Python to calculate the error.

Extra Credit: Create a function in Python which takes two numbers, the numerator and denominator of a fraction, as input and outputs the exact binary representation of the number. Determine some readable way for dealing with repeating values.

Assignment 2:

Question 1. Solve the equations x⁵ - x - 1 = 0 and ln(x) = sin(x) using (a) the bisection method (b) the fixed point method (c) Newton's method (both roots have multiplicity 1) (d) the Secant Method and (e) the built in function fsolve in scipy.optimize. Note that the last part will require a bit of independent Googling as it is something that we didn't cover in class. I think this is GREAT practice for the real world. If you do need help on this however please come to office hours of send me an email! For each function include a table listing your iterations and the approximation of the root, except for (e). Also include a very brief comparison of the methods for these problems.

Fun math fact (unrelated to the work you need to do)! One can show, using a field of math called abstract algebra, that although there are equations to find the roots of polynomials of degrees 2, 3, and 4, there can't be one for 5. This is known as the Abel-Ruffini theorem. Practically, this means that the root you find of x5 x 1 can't actually be written down exactly using "common" operations (think roots, addition, division, etc.). Since this is already the case for polynomials, hopefully this gives you a good idea that in general finding roots not computationally can be very hard or even outright impossible.

Question 2. How many iterations are required of the bisection method, starting with an interval of [ a, b] to approximate a root with accuracy at least 10-6?

Question 3. Consider√f (x) = x/2 + 1/x, g(x) = (2x)/3 + 2/(3x), h(x) = (3x)/4 + 1/(2x). Each of these has a fixed point of √2. Which will converge the fastest using the fixed point method?

Question 4. Find the fixed point iteration produced by Newton's Method on f (x) = x³ - A, where A is an an arbitrary number (a parameter). That is, find a general formula for calculating ³√A.

Question 5. What is the multiplicity of the root at 0 of f (x) = x² sin(x²)? Write down the fixed point iteration produced by modified Newton's method for this problem.

Question 6. A fisher wants to set the net at a water depth where the temperate is 10C. By dropping a line with a thermometer attached, they find that the temperature is 8 degrees at a depth of 9 meters, and 15 degrees at a depth of 5 meters. Use the Secant Method to determine a best estimate for the depth at which the temperature is 10.

Extra Credit: The Mandelbrot set is one of the most interesting and beautiful objects in mathematics. Do a bit of research into this set and discuss how it is generated and what topic it relates to from this chapter.

Assignment 3:

Question 1. In this problem we will create code to solve a matrix using Gaussian elimination without partial pivoting.

(a) Create a function that takes a matrix A, number c and two integers i and j as inputs, and outputs a matrix where row j is replaced with row i times c subtracted from row j.

(b) Using part (a) create a function which takes as input a matrix A and an integer i and eliminates column i. That is, it outputs a matrix using part (a) multiple times where every entry below Ai,i, the diagonal element, are 0.

(c) Create a function with an input of a matrix A that applies (b) multiple times so that the resulting matrix is upper triangular. Note that we are doing Gaussian elimination, so our input is really an augmented matrix, meaning that we have one more column than rows.

(d) Create a function that takes as input a matrix A in upper triangular form and backsolves for your solution. Again, A is not square as we are dealing with an augmented matrix. Hint: Work this out on paper first. You should be able to write down an explicit formula for what your solution should be.

Question 2. What is the condition number of

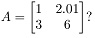
You may use Python to calculate the inverse of the matrix, but if you do so, include your code. Practically, what does this mean when solving the system of equations Ax = b?

Question 3. For each of the matrices, give its PA = LU factorization.

Question 4. Using your answer from (3b) solve the system of linear equations

x + y = 3
2x + y - z = 1
-x + y + z = 3.

Question 5. Apply two steps of Newton's method to approximate the system of non-linear equations:
x² + 4y² = 4,
4x² + y² = 4.
You may use Python to solve any systems of linear equations you need, but if you do please include your code. Start at x₀ = (1,1).

Question 6. (Coding) Create a function which runs Newton's method for k steps on the previous system of equations. Include a table of the approximate solutions.

Extra Credit (Coding): Convert your algorithm from (1) to output the PA = LU factorization of a matrix A. Note that here we are no longer dealing with augments matrices, but instead square matrices. Then, using this algorithm create a function which takes a matrix A and tor b as an input, outputs a solution to Ax = b.