Reference no: EM133124085

CSC 420 Theory of Computation - University of Tabuk

Part 1:

Question 1: Give the following DFAs over ∑ = {a, b}

DFAs recognizes language L1 = L(M1)

DFA1 M₁ for L1

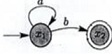
a) Construct a DFA for the language L1*.

b) What is the regular expression (RE) for L1?

Question 2: a) Consider the following NFA-ε over ∑ = {a, b}:

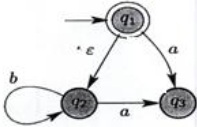
Convert this NFA-ε into DEA.

b) Build NFA for L((ba) U(ab)* over ∑ = (a, b).

Question 3: a) Consider the following CFG:

S→aS|aX|a

X→anX|bS|aa

1) What is the regular expression (RE) accepted by this CFG?

2) Show that whether this CFG is ambiguous or not:

3) Show that whether the word "abaaa" is accepted or not by this CFG:

b) Considering the below PDA, give the (state; stack) evolution of input string w = abb.

Question 4: Convert the following CFG into an equivalent CFG in Chomsky Normal Form(CNF) over the

∑ = {a, b}

S → aS|abX

X → baY

Y → aaX|ε

Part 2:

Question 1: Give DFAs for the following languages over the alphabet is Σ = {a, b}

1) The language L(RE = b*a(ab)*b).

2) The language {w ∈ Σ* | w starts with ab}.

Question 2:

Convert the following CFG into an equivalent CFG in Chomsky Normal Form (CNF) over the

Σ = {a, b}.

S → aS |bbX

X → aaX| bY | ε

Y → aX

Question 3:

Consider the following CFG over {0,1}:
S → 0S | 0X
X → 11X | ε

1) What is the regular expression (RE) accepted by this CFG?

2) Show that whether this CFG is ambiguous or not:

3) Show that whether the word "01111" is accepted or not by this CFG:

4) Convert this CFG into PDA.

Question 4: Consider the following language:

L1 = L(re=0100*)

a) Build a deterministic pushdown automata (PDA) that recognizes this language L1 over the Σ = {0, 1}.

b) Build a Turing Machine(TM) that recognizes this language L1 over the Σ = {0, 1}.