Reference no: EM133066158

Question 1

The ‘Huit Denim' company produces denim in Wales. The fixed monthly cost of the textile mill is £21,000 and the variable cost per yard of denim is £0.45. The mill sells a yard of denim for £1.30.

a) For a monthly volume of 18,000 yards of denim, determine the total cost, total revenue andprofit.

b) Determine the annual break-evenvolume.

c) If the maximum operating capacity is 25,000 yards of denim per month, determine the break-even volume as a percentage ofcapacity.

d) If the variable cost per yard of denim rises to £0.55, what effect will this have on the break-evenvolume?

e) Build a spreadsheet of this break-even problem which captures all of the answers to parts a) to d). Your answer should include screenshots of both the model results view and the formula view, along with some explanatory notes as needed. If ‘Solver' is used in answering this question, a screenshot of the ‘Solver' parameter screen must also be included in theanswer.

Question 2

Analytic Hierarchy Process (AHP) is a useful technique which can aid decision making in the process of selecting potential suppliers.

Use AHP to evaluate which of the three courier service suppliers would best serve a company's needs; the three courier companies are DHM, Post-Fast, and UK Mail.

The two criteria evaluated will be ‘Dependability' and ‘Cost', with the pairwise comparison ratio of 1:3.

Tables 1 and 2 provide data on comparisons for each alternative with respect to the two criteria.

Table 1: Alternatives with respect to Dependability

DHM	1	Post-Fast	5
Post-Fast	1	UK Mail	3
UK Mail	4	DHM	1

Table 2: Alternatives with respect to Cost

DHM	1	Post-Fast	1/5
Post-Fast	1	UK Mail	4
UK Mail	1/7	DHM	1

Question 3

The Swansea Fertiliser Company makes a fertiliser using two chemicals which provide nitrogen, phosphate and potassium.

A pound of ingredient 1 contributes 10 ounces of nitrogen and 6 ounces of phosphate whereas, a pound of ingredient 2 contributes 2 ounces of nitrogen, 6 ounces of phosphate and 1 ounce of potassium.

Ingredient 1 costs £3 per pound (lb) and ingredient 2 costs £5 per pound.

The company wants to know how many pounds of each chemical ingredient to put into a bag of fertiliser in order to meet the minimum requirements of 20 ounces of nitrogen, 36 ounces of phosphate and 2 ounces of potassium while minimising cost.

a) Formulate as a linear programming problem.

b) Solve using a spreadsheet. Your answer should include screenshots of both the model results view and the formula view, along with some explanatory notes as needed. If ‘Solver' is used in answering this question, a screenshot of the ‘Solver' parameter screen must also be included in the answer.

The SoM student business incubator wants to open a ‘pop-up' food store at a local stadium to support the University's football team. There will be six games in the season and a vending fee of £1000 is charged by the stadium per game for rental space.

The students plan to sell cheese pizza slices for £4 and hot dogs for £3. They will purchase 16-inch pizzas (each with 8 slices) from a local pizzeria for £10 which will be delivered twice per game, one hour before kick-off and then again at half-time.

The hot dogs will made in the University catering department, wrap them in foil and deliver them at the same time as the pizzas; however, they only have enough time and kitchen capacity to make 1,000 hot dogs at most.

A budget of £1,000 has been set per game for purchase of the food. They assume each delivery to be sold by the time the next delivery arrives and all items will be sold at the end of the match.

They will need to purchase a warming oven for £2,600 to store the pizza and hot dogs waiting to be sold. The oven has 16 shelves, each with a storage area of 1,728 in2. Pizza boxes and hot dogs cannot be stacked on top of each other on a shelf. A pizza box takes up 324 in2 of space and a hot dog 16 in2.

After conducting some market research at the stadium, they believe they will sell at least 20% more pizza slices than hot dogs.

The students want to determine how many pizzas to order and how many hot dogs to make along with a corresponding profit projection.

c) Formulate a linear programming model for thisproblem.

d) Solve using a spreadsheet. Your answer should include screenshots of both the model results view and the formula view, along with some explanatory notes as needed. If ‘Solver' is used in answering this question, a screenshot of the ‘Solver' parameter screen must also be included in the answer.

e) i) If the students purchase a larger warming oven which has 25 shelves with the same shelf dimensions for an additional £2000, by how much would their profit increase?

ii) If they decided to increase the budget per game by £1500, by how much would their profit increase?

iii) If they increased the selling price of a hot dog to £4 would this result in a greater profit if demand then fell to 600 (at most), due to the higher price?

Question 4

Global Foods Inc., imports food products such as meats, cheese and pastries to the United States from warehouses at ports in Bremen, Toulouse and Cardiff.

Ships from these ports deliver the products to Boston, Miami and Charleston where they are stored in company warehouses before being delivered to distribution centres in Lubbock, Kansas City and Pittsburg.

The products are then distributed to speciality food stores and also sold online. The shipping costs($/1000lb.) from the European ports to the U.S. cities and the available supplies (multiplied by 1,000 lbs.) at the European ports are shown in Table 3:

	U.S. Port
European Port	4. Boston	5. Miami	6. Charleston	Supply
1. Bremen	$420	$390	$610	55
2. Toulouse	$510	$590	$470	78
3. Cardiff	$450	$360	$480	37

Table 3

The transportation costs ($/1000lb.) from each U.S. port to the distribution centres and the demands (multiplied by 1,000 lbs.) at the centres are shown below in Table 4:

	Distribution Centre
Warehouse	7. Lubbock	8. Kansas City	9. Pittsburg
4. Boston	$75	$63	$81
5. Miami	$125	$110	$95
6. Charleston	$68	$82	$95
Demand	60	45	50

Table 4

Construct a spreadsheet to determine the optimal shipments between the European ports and the warehouses and to the distribution centres from the warehouses, in order to minimise total transportation costs.

Your answer should include screenshots of both the model results view and the formula view, along with some explanatory notes as needed. If ‘Solver' is used in answering this question, a screenshot of the ‘Solver' parameter screen must also be included in the answer.

During a large-scale humanitarian crisis in central Asia, large amounts of relief supplies had to be shipped daily from supply depots in Europe. The critical factor in the movement of these supplies was speed.

Table 5 shows the number of planeloads of supplies available each day from each of the six supply depots and the number of daily loads demanded at each of the five airports in Asia. (Each planeload is approximately equal in tonnage).

Also shown are the transport hours per plane (including all loading/unloading, fuelling and flight times).

			Asian Airports
	A	B	C	D	E
Supply Depot						Supply
1	36	40	32	43	29	7
2	28	27	29	40	38	10
3	34	35	41	29	31	8
4	41	42	35	27	36	8
5	25	28	40	34	38	9
6	31	30	43	38	40	6
Demand	9	6	12	8	10

Table 5

Create a spreadsheet to determine the optimal daily flight schedule which will minimise total transport time.

Your answer should include screenshots of both the model results view and the formula view, along with some explanatory notes as needed. If ‘Solver' is used in answering this question, a screenshot of the ‘Solver' parameter screen must also be included in the answer.

Question 5

The Welsh Carpet Company manufactures two brands of carpet - shag and sculptured - in 100-yard rolls. It requires 8 hours to produce one roll of shag carpet and 6 hours to produce a roll of sculptured carpet. The company has the following production goals in prioritised order:

Do not underutilise production capacity which is 480 hours.

Achieve product demand of 40 (100-yard) rolls for shag and 50 (100-yard) rolls for sculptured carpet. Meeting demand for shag is more important than meeting demand for sculptured, by a ratio of 5 to 2.

Limit production overtime to 20 hours.

a) Formulate a goal programming model to determine the amount of shag and sculptured carpet to best meet the company'sgoals.

b) Construct a spreadsheet to solve this problem and present thefindings.

Your answer should include screenshots of both the model results view and the formula view, along with some explanatory notes as needed. If ‘Solver' is used in answering this question, a screenshot of the ‘Solver' parameter screen must also be included in the answer.

Question 6

a) Compute Late Start (LS) and Late Finish (LF) for each node in the following network diagram (Figure 1).

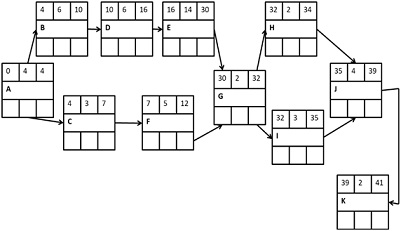
Figure 1: Network Diagram

b) Define slack and then compute the slack for each activity presented in Figure 1.

c) Define the term critical path and then identify the critical path from Figure 1.

Table 6 presents information related to a project that has twelve activities (A to L). Construct a network diagram using Activity-On-Node notation. Determine the normal time it will take to complete the project. Determine the critical path for the project.

Table 6: Information related to project activities

Activity	Immediate Predecessor (s)	Activity Time (weeks)
A	None	10
B	None	4
C	A,B	6
D	A	7
E	B	14
F	C,D,E	3
G	F	4
H	F	2
I	F	5
J	H,I	2
K	J	5
L	K	10

e) Define in detail (with examples), the terms ‘Project' and ‘Project Life Cycle'.

Note: Referenceing APA7th style