Reference no: EM133168953

CSCI 4650 Numerical Analysis - University of Colorado

Question 1. In this problem we will create code to solve a matrix using Gaussian elimination without partial pivoting.

(a) Create a function that takes a matrix A, number c and two integers i and j as inputs, and outputs a matrix where row j is replaced with row i times c subtracted from row j.

(b) Using part (a) create a function which takes as input a matrix A and an integer i and eliminates column i. That is, it outputs a matrix using part (a) multiple times where every entry below Ai,i, the diagonal element, are 0.

(c) Create a function with an input of a matrix A that applies (b) multiple times so that the resulting matrix is upper triangular. Note that we are doing Gaussian elimination, so our input is really an augmented matrix, meaning that we have one more column than rows.

(d) Create a function that takes as input a matrix A in upper triangular form and backsolves for your solution. Again, A is not square as we are dealing with an augmented matrix. Hint: Work this out on paper first. You should be able to write down an explicit formula for what your solution should be.

Question 2. What is the condition number of

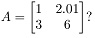
You may use Python to calculate the inverse of the matrix, but if you do so, include your code. Practically, what does this mean when solving the system of equations Ax = b?

Question 3. For each of the matrices, give its PA = LU factorization.

Question 4. Using your answer from (3b) solve the system of linear equations

x + y = 3
2x + y - z = 1
-x + y + z = 3.

Question 5. Apply two steps of Newton's method to approximate the system of non-linear equations:
x² + 4y² = 4,
4x² + y² = 4.
You may use Python to solve any systems of linear equations you need, but if you do please include your code. Start at x₀ = (1,1).

Question 6. (Coding) Create a function which runs Newton's method for k steps on the previous system of equations. Include a table of the approximate solutions.

Extra Credit (Coding): Convert your algorithm from (1) to output the PA = LU factorization of a matrix A. Note that here we are no longer dealing with augments matrices, but instead square matrices. Then, using this algorithm create a function which takes a matrix A and tor b as an input, outputs a solution to Ax = b.