Reference no: EM13243816

Statistics - Inventory Problem

George Madison used to be an accounting professor at a state university. Several years ago, he started to develop seminars and programs for the CPA review course. The CPA review course is a course to help accounting students and others interested in passing the CPA exam. In order to develop an effective seminar, George developed a number of books and other related materials to help. The main product was the CPA review manual developed by George. The manual was an instant success for his seminars and other seminars and courses across the country. Today, George spends most of his time refining and distributing this CPA review manual. Annual demand is 9,600, and the cost of ordering is $400 per order. The price of the manual is $100.00. George's total cost to manufacture and produce the manual is $80.00. George wants to avoid stockouts and/or to develop a stockout policy that would be cost-effective. If there is a stockout on the CPA review manual, George loses the profit from the sale of the manual.

George wants to know how much safety stock he should have as a buffer. George estimates that his carrying cost per unit per year is $12.00. Based upon total cost what ROP and what level of safety stock would you recommend? The frequency of demand for the CPA review manuals during lead time is given in Table 1.

Table 1 Frequency Distribution for Demand

Demand During Lead Time	Frequency (number of times demanded)
350	3
400	2
450	2
500	4
550	5
600	6
650	5
700	5
750	5
800	3

Complete all of the columns in the following table, and explain your recommendation.

ROP (old)	ROP (new)	SS	Ch	Cst	TC

2. Statistics - Project Management

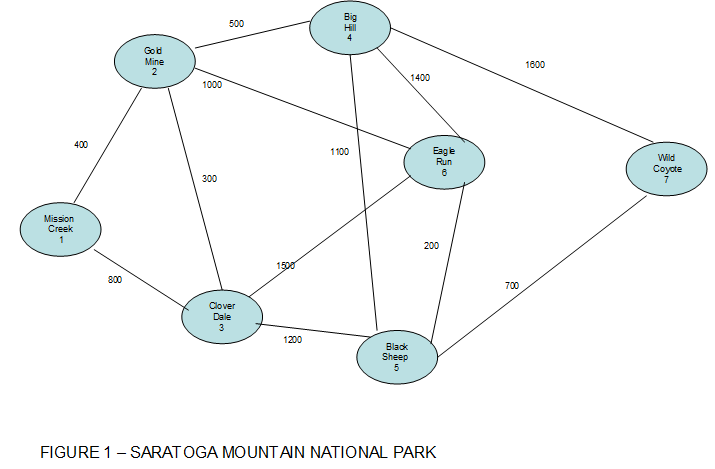
The Department of Interior has named the Saratoga Mountain area a national park. It is in the planning stages of developing a campsite over 500 acres of currently undeveloped land. This campsite will span the extremities of the park, from the proposed Mission Creek Campsite area in the west to the Wild Coyote campsite area in the east. Refer to Figure 1.

At this time, all of the contracts for this project have been awarded. The project has been subdivided into ten individual activities, as shown in Table 1. Based on similar projects, it has been possible to estimate optimistic times, most probable times, and pessimistic times for most activities [Refer to Table 1]. Activities F and I are discussed in the following paragraphs.

Activity F, which will be performed by Ellis Electric, involves laying the electrical cable for the project. To minimize its costs, Ellis Electric will design the system to use the least amount of electrical cable. Ellis will charge the government an amount between $100,000 and $200,000. For $100,000, Ellis Electric can assign enough workers to lay 300 feet of cable per week. For $200,000, Ellis will assign additional workers to lay 500 feet of cable each week. You can determine the number of linear feet based upon minimal spanning.

Activity I involves constructing one (narrow) paved two-lane road from Mission Creek in the west to Wild Coyote in the east. This work will be done by Harriman Construction Company. To minimize the costs, the department will pay Harriman to build the road of minimum distance between the two campsites. At a cost to the government of $25,000 per week, 200 feet of roadway can be completed in a week. If the cost is increased to $36,000 per week, the completion rate will increase to 250 feet per week. You can use shortest path to determine the number of linear feet.

Due to the heavy brush and mountainous nature of the area, 12 possible dirt paths exist between the campsites. Neither Ellis nor Harriman is permitted to clear out additional areas for constructing either underground cable or the paved road. Thus, the electrical cable must be laid and the road must be built along areas of the dirt paths. Figure 1 provides a map of the possible dirt paths between campsites showing distances in feet.

The grand opening of Saratoga Mountain National Park has been schedule for exactly 62 weeks from now. It is imperative that the project be completed within the 62-week period because a delay of even one day in the opening of the park would result in revised travel costs for the dignitaries, lost income to the park, and other expenses.

The Normal Cost column in Table 1 represents how much an activity would cost if completed in the expected time. The Crash Cost column represents the additional cost that would be accrued if the activity was crashed the maximum amount possible.

The Normal Time will be expected time you calculate for each activity. The Max Crash Time represents the maximum amount by which an activity could be crashed. For example if the expected time for an activity is 12 weeks, and the maximum crash time is 2 weeks, that means that the activity could be crashed to 10 weeks, but no more. 

(a) Calculate and show the expected times and variances for each activity [A, B, C, D, E, G, H, J]. Determine times for F and I based upon your calculations of linear feet.

(b) Construct the PERT network for this problem.

(c) Create an Activity Schedule [i.e., table showing ES, EF, LS, LF, slack] for the four options.

(d) What are the activities on the critical path for each option? Explain your answer.

(e) What is the expected completion time for each option?

(f) What is the total cost for each option?

(g) Based upon the costs and times determined for the four options without crashing, which one would you recommend? Explain your.

(h) What is the standard deviation of the critical path in part (d) in each option? Based upon your recommendation in part (g), what is the probability of completing the project at most one week more than the expected time?

(i)  Based upon your recommendation given in part (g), would you suggest crashing any activities to meet the 62-week deadline? Explain your decision.

Table 1. Activities, Immediate Predecessor, Times and Costs

Activity	Immediate Predecessor	Optimistic time	Most Probable time	Pessimistic time	Normal cost	Maximum crash time	Additional crash cost
A		10	15	26	$85,000	11	$80,000
B		10	12	14	$40,000	6	$60,000
C		15	18	33	$90,000	10	$60,000
D	A	20	24	34	$145,000	10	$170,000
E	B	8	10	12	$100,000	6	$120,000
F	C,E
G	F	6	10	14	$200,000	8	$400,000
H	G	8	12	16	$175,000	6	$300,000
I	D, H
J	F	40	40	40	$150,000	20	$350,000