Reference no: EM133131351

Question 1: Consider the Statecharts for a solution to the two-task mutual exclusion problem in Figures 5.3 and 5.4. Statechart A is basically a classical finite-state machine whereas Statechart B takes advantage of Statecharts' features. Show the two cor¬responding Statecharts for a system with three tasks. Describe how Statechart B (for both the two-task and three-task systems) avoids the state-explosion problem found in statechart A.

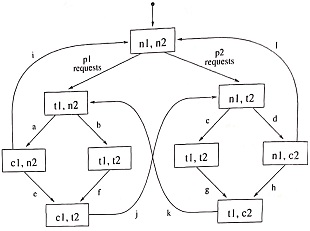
Figure 1: Statechart A of a solution to the mutual exclusion problem.

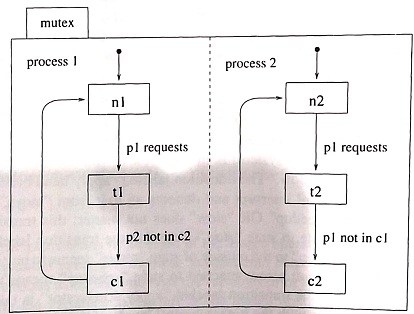
Figure 2: Statechart B of a solution to the mutual exclusion problem

Question 2: Express the following safety assertion in RTL: If the brake actuator is activated (ACTIVATED) within 30 time units of the completion of action TRANSMIT (which transmits the signal from the brake to the brake actuator), we are assured that within 100 time units of pressing the brake (BRAKE), the brake actuator is activated, and within 120 time units of pressing the brake but at least 40 time units after pressing the brake, the braking mechanism will be applied (STOP).

Question 3. If all edges involved in a positive cycle in a constraint graph U correspond to literals that belong to unit clauses, F" (SP ^ ¬SA in clausal form) must be unsatisfiable. If an edge corresponds to a literal that belongs to non-unit disjunctive clause C_i, then it must be shown that each of the remaining literals in C_i; is also involved in a different positive cycle. Explain why this is necessary.

Question 4. Consider the following set of inequalities.

1. t₁ : C ≤ A
2. t₂ : A - 15 ≤ B
3. t₃ : B+ 15 ≤ C
4. t₄v t₆:C-10 ≤ D v B + 10 ≤ D
5. t₅ v t₇: D + 15 ≤ C v D + 15 ≤ B
6. t_{7 v} t₈ :D+ 15 ≤ B v D + 5 ≤ D

(a) Construct the constraint graph for these inequalities.
(b) List the positive cycles.
(c) Using these positive cycles, construct a tree to find out if this set of inequal-ities is unsatisfiable. You might have to check that the inequalities in a leaf node are by themselves not satisfiable.

Question 5. Consider again the specification of the NASA 2001 Mars Odyssey Orbiter (Cams 20011 described in chapter 5 (exercise 81. but now with timing constraints on the different events and actions.

The orbiter is in the ready mode before launch. Before and during launch, the orbiter is folded into a protective housing. The execution time for the launch is 60 s. The start of the launch occurs after a delay of 30 s but within 90 s of the time the orbiter becomes ready.

After launch, the solar panel extends within 120 s to convert solar energy into electric energy for navigational use. When the orbiter approaches Mars after IS months, its engine fires within 20 s and the orbiter inserts into Mars' orbit.

Question 6. Braking starts 50 s after the start of engine firing, and braking takes 20 s. After braiano, the orbiter deploys its high-gain antenna within 100 s. At any time after launch, if an emergency occurs (expected steps are not executed as observed by a specialized monitoring computer), the orbiter skips the above steps and enters a safe mode within 10 s and lets mission controllers take over control of the orbiter. Represent the behavior of the orbiter using (a) RTL

Question 7. Consider the following EQL program:

arbiter := b ! wake_up = false IF (error = a)
[] object_detected := true
IF (sensor_a = 1) AND (arbiter = a) AND (wake_up = true)

[]object_detected := false
IF (sensor_a = 0) AND (arbiter = a) AND (wake_up = true) 0 arbiter := a ! wake_up = false IF (error = b)
[] object_detected := true
IF (sensor_b = 1) AND (arbiter = b) AND (wake_up = true)

[]object_detected := false
IF (sensor_b = 0) AND (arbiter = b) AND (wake_up = true)

Use the general analysis strategy to analyze this program and report the analysis results.

Question 8. Consider a simple algorithm for solving the mutual exclusion problem tor two processes. Construct the state transition diagram for this algorithm. Prove or disprove the following properties by first expressing them in CTL formulas and then by following as much as possible the labeling technique in the CES model checker.
(a) Only one of the two processes can be in the critical section at any one time.
(b) The two processes will not deadlock.