Reference no: EM132246207
Applied Statistics Assignment -
Q1. Determine whether the following sampling is dependent or independent. Indicate whether the response variable is qualitative or quantitative.
A researcher wishes to compare personality types of married lawyers and their spouses. She obtains a random sample of 975 such couples who take a personality inventory and determines each spouse's personality type.
Determine whether the following sampling is dependent or independent.
A. The sampling is independent because an individual selected for one sample does not dictate which individual is to be in the second sample.
B. The sampling is independent because an individual selected for one sample does dictate which individual is to be in the second sample.
C. The sampling is dependent because an individual selected for one sample does not dictate which individual is to be in the second sample.
D. The sampling is dependent because an individual selected for one sample does dictate which individual is to be in the second sample.
Indicate whether the response variable is qualitative or quantitative.
A. The variable is qualitative because it is a numerical measure.
B. The variable is quantitative because it classifies the individual.
C. The variable is quantitative because it is a numerical measure. 0 D. The variable is qualitative because it classifies the individual.
Q2. An educator wants to determine whether a new curriculum significantly improves standardized test scores for fourth grade students. She randomly divides 60 fourth-graders into two groups. Group 1 is taught using the traditional curriculum, while group 2 is taught using the new curriculum. At the end of the school year, both groups are given the standardized test and the mean scores are compared. Determine whether the sampling is dependent or independent. Indicate whether the response variable is qualitative or quantitative.
Determine whether the sampling is dependent or independent.
A. The sampling is dependent because the individuals selected to be in one sample are used to determine the individuals to be in the second sample.
B. This sampling is independent because the individuals selected for one sample do not dictate which individuals are to be in a second sample.
C. The sampling is dependent because the individuals selected for one sample do not dictate which individuals are to be in a second sample.
D. The sampling is independent because the individuals selected to be in one sample are used to determine the individuals to be in the second sample.
Indicate whether the response variable is qualitative or quantitative.
A. The variable is qualitative because it is a numerical measure.
B. The variable is quantitative because it classifies the individual.
C. The variable is quantitative because it is a numerical measure.
D. The variable is qualitative because it classifies the individual.
Q3. Conduct a test at the α = 0.01 level of significance by determining (a) the null and alternative hypotheses, (b) the test statistic, and (c) the P-value. Assume the samples were obtained independently from a large population using simple random sampling.
Test whether p1 > p2. The sample data are x1 = 124, n1 = 253, x2 = 143, and n2 = 306.
(a) Choose the correct null and alternative hypotheses below.
A. H0: p1 = p2 versus H1: p1 ≠ p2
B. H0: p1 = p2 versus H1: p1 > p2
C. H0: p1 = 0 versus H1: p1 ≠ 0
D. H0: p1 = p2 versus H1: p1 < p2
(b) Determine the test statistic.
(c) Determine the P-value.
What is the result of this hypothesis test?
A. Do not reject the null hypothesis because there is not sufficient evidence to conclude that p1 ≠ p2.
B. Do not reject the null hypothesis because there is not sufficient evidence to conclude that p1 < p2.
C. Do not reject the null hypothesis because there is not sufficient evidence to conclude that p1 > p2.
D. Reject the null hypothesis because there is sufficient evidence to conclude that p1 < p2.
Q4. Construct a confidence interval for p1 - p2 at the given level of confidence.
x1 = 393, n1 = 546, x2 = 409, n2 = 554, 90% confidence
The researchers are ________ % confident the difference between the two population proportions, p1 - p2, is between _____ and _____. (Use ascending order. Type an integer or decimal rounded to three decimal places as needed.)
Q5. In 1950, an organization surveyed 1100 adults and asked, "Are you a total abstainer from, or do you on occasion consume, alcoholic beverages?" Of the 1100 adults surveyed, 418 indicated that they were total abstainers. In a recent survey, the same question was asked of 1100 adults and 385 indicated that they were total abstainers.
Complete parts (a) and (b) below.
(a) Determine the sample proportion for each sample.
The proportions of the adults who took the 1950 survey and the recent survey who were total abstainers are _______ and ________, respectively.
(b) Has the proportion of adults who totally abstain from alcohol changed? Use the α = 0.01 level of significance. First verify the model requirements. Select all that apply.
A. The sample size is more than 5% of the population size for each sample.
B. The samples are dependent.
C. The samples are independent.
D. The data come from a population that is normally distributed.
E. The sample size is less than 5% of the population size for each sample.
F. n1p^1 (1 - p^1) ≥ 10 and n2p^2 (1 - p^2) ≥ 10
Identify the null and alternative hypotheses for this test. Let p1 represent the population proportion of 1950 adults who were total abstainers and p2 represent the population proportion of recent adults who were total abstainers.
Determine the null and alternative hypotheses.
H0: p1 (1) _______ p2
H1: p1 (2) ______ P2
Find the test statistic for this hypothesis test.
Determine the P-value for this hypothesis test.
Interpret the P-value.
If the population proportions are (3) ________ one would expect a sample difference proportion (4) _______ the one observed in about ________ out of 100 repetitions of this experiment.
State the conclusion for this hypothesis test.
A. Reject H0. There is sufficient evidence at the α = 0.01 level of significance to suggest the proportion of adults who totally abstain from alcohol has changed.
B. Do not reject H0. There is sufficient evidence at the α = 0.01 level of significance to suggest the proportion of adults who totally abstain from alcohol has changed.
C. Do not reject H0. There is not sufficient evidence at the α = 0.01 level of significance to suggest the proportion of adults who totally abstain from alcohol has changed.
D. Reject H0. There is not sufficient evidence at the α = 0.01 level of significance to suggest the
(1) <, ≠, =, >
(2) ≠, <, >, =
(3) equal, not equal
(4) greater than the absolute value of, greater than, smaller than the absolute value of, smaller than
Q6. Assume that the differences are normally distributed. Complete parts (a) through (d) below.
|
Observation
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
Xi
|
41.4
|
53.7
|
50.9
|
48.2
|
44.0
|
44.5
|
50.6
|
51.9
|
|
Yi
|
54.8
|
54.8
|
53.1
|
52.9
|
46.7
|
47.2
|
53.9
|
53.6
|
(a) Determine di = Xi - Yi for each pair of data.
(b) Compute d- and sd.
(c) Test if μd < 0 at the α = 0.05 level of significance.
What are the correct null and alternative hypotheses?
A. H0: µd > 0
H1: µd < 0
B. H0: µd < 0
H1: µd = 0
C. H0: µd = 0
H1: µd < 0
D. H0: µd < 0
H1: µd > 0
P-value = ________ (Round to three decimal places as needed.)
Choose the correct conclusion below.
A. Reject the null hypothesis. There is insufficient evidence that µd < 0 at the α = 0.05 level of significance.
B. Do not reject the null hypothesis. There is sufficient evidence that lid μd < 0 at the α = 0.05 level of significance.
C. Reject the null hypothesis. There is sufficient evidence that µd < 0 at the α = 0.05 level of significance.
D. Do not reject the null hypothesis. There is insufficient evidence that μd < 0 at the α = 0.05 level of significance.
(d) Compute a 95% confidence interval about the population mean difference μd.
The lower bound is _______.
The upper bound is _______.
Q7. The following data represent the muzzle velocity (in feet per second) of rounds fired from a 155-mm gun. For each round, two measurements of the velocity were recorded using two different measuring devices, resulting in the following data. Complete parts (a) through (d) below.
|
Observation
|
1
|
2
|
3
|
4
|
5
|
6
|
|
A
|
793.5
|
794.6
|
793.5
|
791.9
|
793.2
|
793.7
|
|
B
|
799.8
|
792.5
|
802.0
|
788.1
|
795.8
|
789.9
|
(a) Why are these matched-pairs data?
A. Two measurements (A and B) are taken on the same round.
B. The same round was fired in every trial.
C. The measurements (A and B) are taken by the same instrument.
D. All the measurements came from rounds fired from the same gun.
(b) Is there a difference in the measurement of the muzzle velocity between device A and device B at the α = 0.01 level of significance? Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers.
Let di = Ai - Bi. Identify the null and alternative hypotheses.
H0: μd (1) ________
H1: μd (2) _______
Determine the test statistic for this hypothesis test.
Find the P-value.
What is your conclusion regarding H0?
(3) ________ H0. There (4) ________ sufficient evidence at the α = 0.01 level of significance to conclude that there is a difference in the measurements of velocity between device A and device B.
(c) Construct a 99% confidence interval about the population mean difference. Compute the difference as device A minus device B. Interpret your results.
The lower bound is ___________.
The upper bound is ___________.
Interpret the confidence interval. Choose the correct answer below.
A. One can be 99% confident that the mean difference in measurement is 0.
B. One can be 99% confident that the mean difference in measurement is 0.01.
C. One can be 99% confident that the mean difference in measurement lies in the interval found above.
D. One can be 1 % confident that the mean difference in measurement lies in the interval found above.
d) Draw a boxplot of the differenced data. Does this visual evidence support the results obtained in part (b)?
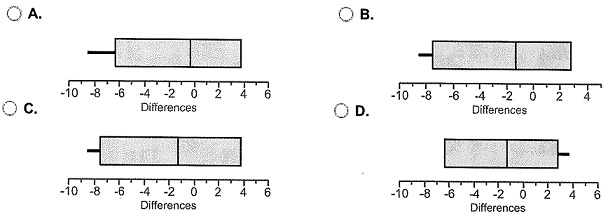
Does this visual evidence support the results obtained in part (b)?
A. Yes, because the boxplot shows no outliers.
B. Yes, because 0 is contained in the boxplot.
C. No, because the boxplot is too large.
D. No, because 0 is not contained in the boxplot.
(1) =, ≠, <, >
(2) <, =, ≠, >
(3) Do not reject, Reject
(4) is, is not
Q8. To test the belief that sons are taller than their fathers, a student randomly selects 13 fathers who have adult male children. She records the height of both the father and son in inches and obtains the following data. Are sons taller than their fathers? Use the α = 0.10 level of significance. Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers.
Table of height data
|
Height of
Father, Xi
|
Height of Son, Yi
|
|
67.8
|
72.9
|
|
68.8
|
72.2
|
|
72.3
|
74.9
|
|
72.8
|
74.6
|
|
68.7
|
69.9
|
|
67.9
|
68.4
|
|
72.8
|
72.7
|
|
68.9
|
68.3
|
|
73.1
|
71.9
|
|
70.3
|
68.5
|
|
68.3
|
65.9
|
|
67.2
|
63.7
|
|
68.2
|
63.3
|
Which conditions must be met by the sample for this test? Select all that apply.
A. The differences are normally distributed or the sample size is large.
B. The sampling method results in a dependent sample.
C. The sample size must be large.
D. The sampling method results in an independent sample.
E. The sample size is no more than 5% of the population size.
Let di = Xi - Yi. Write the hypotheses for the test.
H0: (1) ________
H1: (2) _______
Calculate the test statistic.
Calculate the P-value.
Should the null hypothesis be rejected?
(3) ______ H0 because the P-value is (4) ______ the level of significance. There (5) ______ sufficient evidence to conclude that sons (6) ______ their fathers at the 0.10 level of significance.
(1) μd < 0, μd ≠ 0, μd =0, μd > 0
(2) μd = 0, μd > 0, μd ≠ 0, μd < 0
(3) Do not reject, Reject
(4) less then, greater then
(5) is not, is
(6) are shorter than, are the same height as, are taller than, are not the same height as.
Q9. The manufacturer of hardness testing equipment uses steel-ball indenters to penetrate metal that is being tested. However, the manufacturer thinks it would be better to use a diamond indenter so that all types of metal can be tested. Because of differences between the two types of indenters, it is suspected that the two methods will produce different hardness readings. The metal specimens to be tested are large enough so that two indentions can be made. Therefore, the manufacturer uses both indenters on each specimen and compares the hardness readings. Construct a 95% confidence interval to judge whether the two indenters result in different measurements.
Note: A normal probability plot and boxplot of the data indicate that the differences are approximately normally distributed with no outliers.
Data Table -
|
Specimen
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Steel ball
|
50
|
57
|
61
|
71
|
68
|
54
|
65
|
51
|
53
|
|
Diamond
|
52
|
55
|
53
|
74
|
69
|
56
|
68
|
51
|
56
|
Construct a 95% confidence interval to judge whether the two indenters result in different measurements, where the differences are computed as 'diamond minus steel ball'.
The lower bound is ________.
The upper bound is ________.
State the appropriate conclusion. Choose the correct answer below.
There is insufficient evidence to conclude that the two indenters produce different hardness readings.
There is sufficient evidence to conclude that the two indenters produce different hardness readings.
Q10. Use the given statistics to complete parts (a) and (b). Assume that the populations are normally distributed.
(a) Test whether µ1 > µ2 at the μ = 0.05 level of significance for the given sample data.
(b) Construct a 99% confidence interval about μ1 - μ2.
|
|
Population 1
|
Population 2
|
|
n
|
22
|
15
|
|
x-
|
47.2
|
42.3
|
|
s
|
5.9
|
11.4
|
(a) Identify the null and alternative hypotheses for this test.
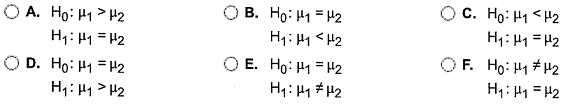
Find the test statistic for this hypothesis test.
Determine the P-value for this hypothesis test.
State the conclusion for this hypothesis test.
A. Reject H0. There is sufficient evidence at the α = 0.05 level of significance to conclude that μ1 > μ2.
B. Do not reject H0. There is sufficient evidence at the α = 0.05 level of significance to conclude that μ1 > μ2.
C. Do not reject H0. There is not sufficient evidence at the α = 0.05 level of significance to conclude that µ1 > μ2.
D. Reject H0. There is not sufficient evidence at the α = 0.05 level of significance to conclude that μ1 > μ2.
(b) The 99% confidence interval about μ1 - μ2 is the range from a lower bound of _______ to an upper bound of _________.
Q11. Test whether μ1 < μ2 at the α = 0.05 level of significance for the sample data shown in the accompanying table. Assume that the populations are normally distributed.
Sample Data
|
|
Population 1
|
Population 2
|
|
n
|
31
|
25
|
|
x-
|
103.5
|
114.2
|
|
s
|
12.3
|
13.2
|
Determine the null and alternative hypothesis for this test.
A. H0: μ1 = μ2
H1: μ1 < μ2
B. H0: μ1 < μ2
H1: μ1 = μ2
C. H0: μ1 ≠ μ2
H1: μ1 < μ2
D. H0: μ1 = μ2
H1: µ1 ≠ μ2
Determine the P-value for this hypothesis test.
State the appropriate conclusion. Choose the correct answer below.
A. Do not reject H0. There is not sufficient evidence at the α = 0.05 level of significance to conclude that μ1 < μ2.
B. Reject H0. There is sufficient evidence at the α = 0.05 level of significance to conclude that μ1 < μ2.
C. Reject H0. There is not sufficient evidence at the α = 0.05 level of significance to conclude that μ1 < μ2.
D. Do not reject H0. There is sufficient evidence at the α = 0.05 level of significance to conclude that μ1 < μ2.
Q12. Ramp metering is a traffic engineering idea that requires cars entering a freeway to stop for a certain period of time before joining the traffic flow. The theory is that ramp metering controls the number of cars on the freeway and the number of cars accessing the freeway, resulting in a freer flow of cars, which ultimately results in faster travel times. To test whether ramp metering is effective in reducing travel times, engineers conducted an experiment in which a section of freeway had ramp meters installed on the on-ramps. The response variable for the study was speed of the vehicles. A random sample of 15 cars on the highway for a Monday at 6 p.m. with the ramp meters on and a second random sample of 15 cars on a different Monday at 6 p.m. with the meters off resulted in the following speeds (in miles per hour).
Speed data (in MPH)
|
Ramp Meters On
|
Ramp Meters Off
|
|
27
|
47
|
55
|
24
|
26
|
43
|
|
38
|
30
|
25
|
34
|
36
|
31
|
|
44
|
47
|
51
|
46
|
38
|
17
|
|
36
|
54
|
41
|
29
|
23
|
41
|
|
42
|
26
|
48
|
38
|
51
|
40
|
(a) Draw side-by-side boxplots of each data set. Does there appear to be a difference in the speeds? Are there any outliers? Choose the correct box plot below.
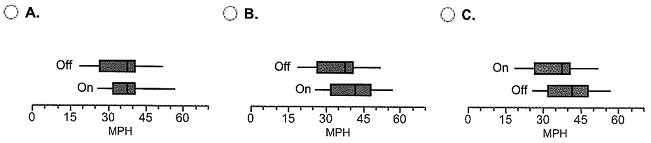
Does there appear to be a difference in the speeds?
A. Yes, the Meters Off data appear to have higher speeds.
B. Yes, the Meters On data appear to have higher speeds.
C. No, the box plots do not show any difference in speeds.
Are there any outliers?
A. No, there does not appear to be any outliers.
B. Yes, there appears to be a high outlier in the Meters On data.
C. Yes, there appears to be a high outlier in the Meters Off data.
D. Yes, there appears to be a low outlier in the Meters On data.
(b) Are the ramp meters effective in maintaining a higher speed on the freeway? Use the α = 0.01 level of significance. State the null and alternative hypotheses. Choose the correct answer below.
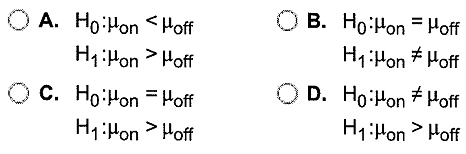
Determine the P-value for this test.
Choose the correct conclusion.
A. Do not reject H0. There is not sufficient evidence at the α = 0.01 level of significance that the ramp meters are effective in maintaining higher speed on the freeway.
B. Do not reject H0. There is sufficient evidence at the α = 0.01 level of significance that the ramp meters are effective in maintaining higher speed on the freeway.
C. Reject H0. There is not sufficient evidence at the α = 0.01 level of significance that the ramp meters are effective in maintaining higher speed on the freeway.
D. Reject H0. There is sufficient evidence at the α = 0.01 level of significance that the ramp.
Q13. A researcher wanted to determine if carpeted rooms contain more bacteria than uncarpeted rooms. The table shows the results for the number of bacteria per cubic foot for both types of rooms.
|
Carpeted
|
Uncarpeted
|
|
15.2
|
13.9
|
14.6
|
13
|
4.3
|
11.2
|
|
9.7
|
6.3
|
9.4
|
5.3
|
10.1
|
13.4
|
|
6.9
|
7.9
|
|
10.9
|
12.8
|
|
Determine whether carpeted rooms have more bacteria than uncarpeted rooms at the α = 0.01 level of significance. Normal probability plots indicate that the data are approximately normal and boxplots indicate that there are no outliers.
State the null and alternative hypotheses. Let population 1 be carpeted rooms and population 2 be uncarpeted rooms.
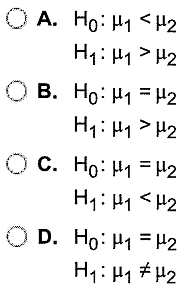
Determine the P-value for this hypothesis test.
State the appropriate conclusion. Choose the correct answer below.
A. Do not reject H0. There is significant evidence at the α = 0.01 level of significance to conclude that carpeted rooms have more bacteria than uncarpeted rooms.
B. Do not reject H0. There is not significant evidence at the α = 0.01 level of significance to conclude that carpeted rooms have more bacteria than uncarpeted rooms.
C. Reject H0. There is significant evidence at the α = 0.01 level of significance to conclude that carpeted rooms have more bacteria than uncarpeted rooms.
D. Reject H0. There is not significant evidence at the α = 0.01 level of significance to conclude that carpeted rooms have more bacteria than uncarpeted rooms.
Q14. Do women feel differently from men when it comes to tax rates? One question on a survey of randomly selected adults asked, "What percent of income do you believe individuals should pay in income tax?"
Survey Results
|
Gender
|
Tax Rate
|
Gender
|
Tax Rate
|
|
Female
|
10
|
Male
|
15
|
|
Female
|
10
|
Male
|
20
|
|
Female
|
5
|
Male
|
9
|
|
Female
|
19
|
Male
|
10
|
|
Female
|
21
|
Male
|
17
|
|
Female
|
15
|
Male
|
2
|
|
Female
|
9
|
Male
|
1
|
|
Female
|
15
|
Male
|
15
|
|
Female
|
3
|
Male
|
3
|
|
Female
|
5
|
Male
|
8
|
|
Female
|
24
|
Male
|
15
|
|
Female
|
10
|
Male
|
5
|
|
Female
|
0
|
Male
|
16
|
|
Female
|
21
|
Male
|
34
|
|
Female
|
10
|
Male
|
10
|
|
Female
|
0
|
Male
|
15
|
|
Female
|
8
|
Male
|
2
|
|
Female
|
20
|
Male
|
0
|
|
Female
|
14
|
Male
|
4
|
|
Female
|
12
|
Male
|
7
|
|
Female
|
20
|
Male
|
15
|
|
Female
|
15
|
Male
|
6
|
|
Female
|
9
|
Male
|
10
|
|
Female
|
14
|
Male
|
5
|
|
Female
|
5
|
Male
|
10
|
|
Female
|
14
|
Male
|
23
|
|
Female
|
15
|
Male
|
15
|
|
Female
|
5
|
Male
|
16
|
|
Female
|
17
|
Male
|
8
|
|
Female
|
23
|
Male
|
10
|
Complete parts a) through c).
a) Draw side-by-side boxplots of tax rates by gender. Choose the correct graph below.
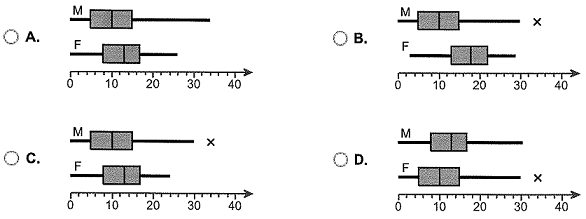
Does there appear to be a difference in the income tax rates between genders?
A. Yes because the income tax rate for females appears to have a higher median than the income tax rate for males.
B. No but the maximum income tax rate for males is higher than the maximum income tax rate for females.
C. No because the income tax rate is about the same for males and females.
D. Yes because the income tax rate for males appears to have a higher median than the income tax rate for females.
b) Explain why a hypothesis test may be used to test whether the mean tax rates for the two genders differ. Select all that apply.
A. Each sample is obtained independently of the other.
B. Each sample size is large.
C. Each sample size is small relative to the size of its population.
D. Each sample is a simple random sample.
E. Each sample has the same sample size.
c) Test whether the mean tax rate for females differs from that of males at the α = 0.01 level of significance.
Determine the null and alternative hypotheses for this test. Let μM represent the mean income tax rate for males and let μF represent the mean income tax rate for females.
H0: (1) ________ (2) ________ (3) ________ versus H1: (4) ________ (5) ________ (6) ________.
Find t0, the test statistic for this hypothesis test.
Determine the P-value for this test.
State the appropriate conclusion. Choose the correct answer below.
A. Do not reject H0. There is sufficient evidence at the level of significance to conclude that the mean income tax rate for males is different from the mean income tax rate for females.
B. Reject H0. There is sufficient evidence at the level of significance to conclude that the mean income tax rate for males is different from the mean income tax rate for females.
C. Reject H0. There is not sufficient evidence at the level of significance to conclude that the mean income tax rate for males is different from the mean income tax rate for females.
D. Do not reject H0. There is not sufficient evidence at the level of significance to conclude that the mean income tax rate for males is different from the mean income tax rate for females.
(1) σM, p, μM
(2) ≠, =, <, >
(3) μF, p0, σF
(4) μM, σM, p
(5) <, =, >, ≠
(6) p0, σF, μF