Reference no: EM13845100
Problem 1: In class we discussed the following properties of z-scores: μZ = 0 (the mean of the Z-scores is 0) σZ = 1 (the standard deviation of the Z-scores is 1) For perfect correlation, Zx = Zy, r=1 Using the definitions of Z-score, mean, standard deviation, and correlation based on Zscore (use the equations for a population), prove these properties. For the last 2 proofs, you will need to use the additional property that Σz2 = N
Problem 2: Construct a scatter plot of the following data using Minitab:
|
x
|
y
|
|
2
|
3
|
|
3.5
|
3.5
|
|
4
|
5
|
|
5
|
3
|
|
3
|
3
|
|
2
|
4
|
|
5
|
4
|
|
3
|
2
|
|
3
|
5
|
|
4
|
4
|
|
2.5
|
4.5
|
|
4
|
3
|
|
4.5
|
2.5
|
|
4
|
3
|
|
4.5
|
4.5
|
|
3
|
4
|
|
2.5
|
2.5
|
|
4
|
2
|
In analyzing this data set, would you calculate a correlation coefficient? Why or why not?
Problem 3: (Montgomery 2-52)
Establishing the properties of materials is an important problem in identifying a suitable substitute for biodegradable materials in the fast-food packaging industry. Consider the following data on product density (g/cm3) and thermal conductivity K- factor (W/mK) published in Materials Research and Innovation (1999, pp.2-8)
|
Density (g/cm3)
|
Thermal Conductivity (W/mK)
|
|
0.1750
|
0.0480
0.0525
0.0540
0.0535
0.0570
0.0610
|
|
0.2200
|
|
0.2250
|
|
0.2260
|
|
0.2500
|
|
0.2765
|
(a) Create a scatter diagram of the data in Minitab, with density as the x-variable and conductivity the y. What do you anticipate will be the sign of the correlation coefficient?
(b) Compute the correlation coefficient (by hand or by generating a spreadsheet in Excel or another program), using whatever method you choose. Based on your answer, what type of linear relationship does the data display (strong, weak, or moderate)?
(c) Check your answer to part b using Minitab
Problem 4: Give an example of a situation in which you might observe a very strong correlation for two variables, but no causation (like the reading level vs. shoe size example discussed in class)
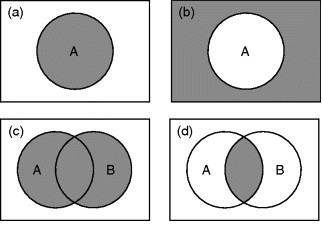
Problem 5: Venn diagrams are a useful tool for understanding sample spaces and relationships among events. Consider the following events:
A - A certain student is enrolled in CHE 445 B - That student is enrolled in CHE 472
Examine the Venn diagrams shown below. Write what situation each diagram depicts in terms of a sentence in English, and write the probability of the events represented in the diagram using the probability notation discussed in class.
Problem 6: Use Venn diagrams to show, visually, that (A ∪ B)′ = A′ ∩ B′. Shading with different colors may be helpful.
Problem 7: Consider a fair deck of 52 cards.
(a) Draw 2 cards. Find the probability that the second card drawn will be a club. Show your work. There are two possible ways for this to happen, which we define as events A and B:
A - first card is a club, 2nd card is a club
B - first card is not a club, 2nd card is a club
(b) Starting with a newly shuffled fair deck, by using the same logic, draw 3 cards and find the probability that the 3rd card drawn will be a spade. Define the events that could lead to this outcome, and show your calculations.
(c) Based on your answers above, and your intuition, state the probability that, for a newly shuffled full deck, the 47th card drawn will be a diamond. Justify your answer.