Reference no: EM132039

Use the following information for Questions 1 -10

Customer	Gender	Payment	Amount Purchased
1	Female	Cash	$23.26
2	Female	Credit	$23.38
3	Female	Credit	$12.50
4	Male	Cash	$10.65
5	Male	Debit	$5.48
6	Female	Credit	$10.81
7	Male	Cash	$17.29
8	Female	Credit	$24.20
9	Female	Debit	$19.37
10	Female	Credit	$11.14
11	Male	Cash	$10.87
12	Male	Credit	$11.43
13	Female	Cash	$18.65
14	Male	Credit	$23.57
15	Male	Cash	$17.19
16	Female	Debit	$6.84
17	Female	Credit	$13.60
18	Female	Debit	$10.50
19	Male	Cash	$16.26
20	Female	Credit	$12.90

Question 1) Which of the following variables are quantitative?

A.    Payment Method

B.     Gender

C.     Amount Purchased

D.    Payment Method and Gender

Question 2) Which of the following variables is measured on the nominal scale?

A.    Amount Purchased

B.     Customer

C.     Gender

D.    Payment method and Gender

Question 3) This data most likely came from?

A.    Focus group

B.     Direct observation

C.     Experiment

D.    Survey

Question 4) Assume the data was collected by randomly selecting 20 customers, data collected represents?

A.    Sample data

B.     Population and Time Series data

C.     Inferential data

D.    Time Series data

Question 5) Construct a frequency distribution for Payment method, how many customers paid with a credit card?

A.    9

B.     7

C.     6

D.    5

Question 6) Based on the cross tabulation table of gender vs. amount purchased, which of the following statements is true?

A.    The amount of purchase (in dollars) by males and females is about the same

B.     Females purchased more (in dollars) than males

C.     Males purchased more (in dollars) than females

D.    None of the above is correct

Question 7) Which cross-tabulation table is correct?

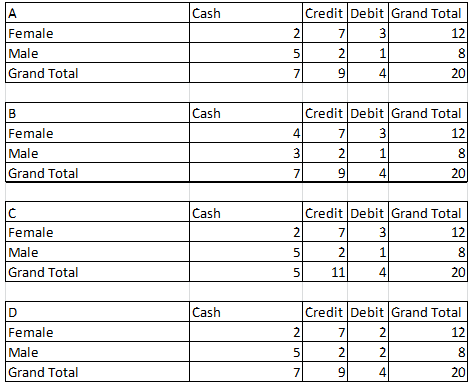
8)      Which of the following stem and leave displays for amount purchased is correct? You may use PHStat2.

 

Question 9) Which two variables would be appropriate to plot in a scatter diagram?

A.    Gender and payment method

B.     Customer and amount purchased

C.     Amount purchased and loyalty club

D.    None of the above is correct

Question 10) If you were to construct a frequency distribution for amount purchased, what would be the class width using method recommended in your book?

A.    2

B.     3

C.     4

D.    5

Use the following data to answer questions 11-15:

A sample of employees participated in a survey of job satisfaction provided information about their hourly wages as the following:

28	11	28	19	28
15	14	13	23	29
14	21	29	27	29
17	23	24	18	22
28	22	28	19	26
25	11	27	20	18
28	13	18	27	23
22	28	12	16	11
16	23	15	15	23
28	27	11	22	26

Question 11) What is the median hourly wage of employees participating in this survey?

A.    21.5

B.     22

C.     22.5

D.    None of the above

Question 12) What is the 70^th percentile of the employee hourly wages? Use the method explained in textbook for answering this question.

A.    26

B.     26.3

C.     26.5

D.    27

Question 13) What is the standard deviation of hourly wages for this sample of employees?

A.    35.22

B.     24.8

C.     6.18

D.    5.96

Question 14) For this sample, what is the minimum number of employees who might receive a salary within two standard deviations from the mean? Use Chebyshev's Theorem to answer this question and round answer to nearest integer.

A. 38
B. 8
C. 12
D. 13

Question 15) A second sample of same size is taken from the same group of employees. It has the same mean and standard-deviation as the earlier sample, but now we assume that hourly wages are bell-shaped. Use the Empirical Rule, to find for the second sample, the maximum number of employees you would expect to receive a wage at least two standard deviations above the mean. Round your answer to the nearest integer.

A. 1
B. 2
C. 3
D. 4

Use this information to answer questions 16 and 17:

AFC trucking Inc. keeps mileage records when changing tires to determine the average life of each brand, in order to optimize their costs of purchasing and replacing tires.  Lifetime of a tire depends on quality of the tire, quality of the road, temperature, and weight of the cargo.  During the past 12 months AFC have collected data about a new type of BFGoodrichtires, summarized as the following:

Mileage used	Number of tires
40000 to under 45000	175
45000 to under 50000	173
50000 to under 55000	170
55000 to under 60000	160
60000 to under 65000	209
65000 to under 70000	229

Question 16) What is the average life of each tire? 

A.    Less than 50,000 miles

B.     Greater than or equal to 50,000 but less than 55,000 miles

C.     Greater than or equal to 55,000 but less than 60,000 miles

D.    Greater than or 60,000 miles

Question 17) What is the standard deviation of recorded mileages for these tires?

A.    Less than 7,000 miles

B.     Greater than or equal to 7,000 but less than 7,500 miles

C.     Greater than or equal to 7,500 but less than 8,000 miles

D.    Greater than 8,500 miles

Use the following data to answer questions 18-20:

This table listsALLice cream flavors sold at Hayley's Ice Cream shop in Okoboji, Iowa and the number of gallons of eachsold duringthis year and last year's summer.

Flavor	Total Gallons Sold ThisSummer	Total Gallons Sold Last Summer
Vanilla	37,259	55,343
Chocolate	107,948	76,855
Strawberry	25,539	22,436
Maple Walnut	15,618	11,432
Praline	19,512	14,609
Butter Pecan	8,836	16,253
Chocolate Chip	36,889	35,395
Mint Chocolate Chip	16,167	18,935
Cookie Dough	24,674	23,443
Rocky Road	18,103	16,496
Fudge Swirl	21,637	18,394
Peach	21,979	23,504

Question 18) Find the interquartile range (IQR) for last year sales of different flavors, using the manual method discussed in your textbook.  This value is:

A.    Less than 12,000

B.     Greater than or equal to 12,000 but less than 13,000

C.     Greater than or equal to 13,000 but less than 14,000

D.    Greater than 14,000

Question 19) Consider this year's sales only. What is the Z score for Maple Walnut flavor sales?

1. Less than 0.5
2. Greater than or equal to 0.5 but less than 0.6
3. Greater than or equal to 0.6 but less than 0.7
4. Greater than 0.7

Question 20)  Which year's sales statistics are more consistent?

1. Last summer, because variance of sales for last summer is smaller than this year's sales
2. Current summer, because standard deviation of sales is greater than last year's sales          
3. Current summer, because coefficient of variation for current summer is greater than last year
4. Last summer, because coefficient of variation for this summer is greater than lastsummer

Use the following information for Questions 21 - 22. Carry out calculations to 4 decimals.

In developing their warranty policy, an automobile company estimates that over a 1-year period 17% of their new cars will need to be repaired once, 7% will need repairs twice, and 4% will require three or more repairs. You and your spouse each buy a new car.

Question 21)  What is the probability that both will need repair in the first year?

A.    0.0784

B.     0.4816

C.     0.5184

D.    0.56

E.     0.96

Question 22)  What is the probability that at least one car will need repair in the first year?

A.    0.0784

B.     0.4816

C.     0.5184

D.    0.56

E.     0.96

Use the following information for Questions 23 - 24.

A GfK Roper Worldwide survey in 2005 asked consumers in 5 countries whether they agreed with the statement "I am worried about the safety of the food I eat." Here are the responses classified by the age of the responded. If we select a person at random from this sample:

		Agree	Neither Agree nor Disagree	Disagree	Don't Know/ No Response	Total
Age	13-19	661	368	452	32	1513
	20-29	816	365	336	16	1533
	30-39	871	355	290	9	1525
	40-49	914	335	266	6	1521
	50+	966	339	283	10	1598
Total		4228	1762	1627	73	7690

Question 23)  What is the probability that the person is younger than 50 years oldand agrees with the statement?

1. 0.9178
2. 0.7922
3. 0.7715
4. 0.5498
5. 0.4242

Question 24)  What is the probability that the person is younger than 50 years old or agrees with the statement?

1. 0.9178
2. 0.7922
3. 0.7715
4. 0.5498
5. 0.4242

Use the following information for Questions 25 - 27.

Personal electronic devices are getting smaller all the time. Manufacturing components for these devices is a challenge, and at the same time, consumers are demanding more and more functionality and increasing sturdiness. Microscopic and even submicroscopic flaws can develop during their fabrication that can blank out pixels on the screens or cause intermittent performance failures. Defects will always occur, so the quality engineer in charge of the production process must monitor the number of defects and take action if the process seems out of control.

An engineer is called down to the production line because the number of defects has crossed a threshold and the process has been declared to be out of control. She must decide between two possible actions. She knows that a small adjustment to the robots that assemble the components can fix a variety of problems. But for more complex problems, the entire production line needs to be shut down in order to pinpoint the problem. The small adjustment requires that production be stopped for about an hour. But shutting down the line takes at least an entire shift (8 hours). Naturally, her boss would prefer that she make the small adjustment. But without knowing the source or severity of the problem, she can't be sure whether that will be successful. The engineer uses her knowledge of probability to predict whether the small adjustment will work.

Based on her experience, the engineer thinks that there are three possible problems: (1) the motherboards could have faulty connections, (2) the memory could be the source of the faulty connections, or (3) some of the cases may simply be seating incorrectly in the assembly line. She knows from past experience how often these types of problems crop up and how likely it is that a small adjustment will fix each type of problem.

Motherboard problems are rare (10%). Memory problems have been showing up about 30% of the time. Case alignments issues occur most often (60%).

The engineer knows the probability is only 0.1 that asmall adjustment will fix the problem if it is due to motherboard. Also, she and her team assess the probability that a small adjustment will fix the problem to be 0.5 if it is due to memory and 0.8 if it is due to case alignment.

The engineer is called to the line because the number of defects has exceeded the threshold.

Question 25)  What is the probability that it is a motherboard problem and cannot be fixed with a small adjustment?

A.    0.01

B.     0.09

C.     0.20

D.    0.90

E.     1.00

Question 26)  Estimate the probability that the problem can be fixed with a small adjustment to the robots.

1. 0.40
2. 0.04
3. 0.64
4. 1.40

Question 27)  Assume she makes the small adjustment to the robots and the problem is fixed. What is the probability that the problem was with the cases?

1. 0.33
2. 0.48
3. 0.50
4. 0.75

Use the following information to answer Questions 28 - 30.

A Human Resource office is drafting an online job application for a particular position within the company. A part of the form lists 3 categories, each with several options under it.

Second Language Skills	Logic/Reasoning Skills	Computer Skills
French	Critical Thinking	Excel
Spanish	Complex Problem Solving	Access
Chinese	Analytical Reasoning	SAS
	Judgment/Decision Making	SAP
	Mathematics

Question 28)  In one part of the form the applicant is instructed to mark his/her strength in each category (one mark under each category).How many different ways are possible for an application to be marked?

A.    12

B.     60

C.     220

D.    1320

Question 29)  In a different part of the form, the applicant is instructed to consider the Logic/Reasoning Skills set and pick 2 of the 5 listed which best represent his abilities. How many different ways can a random applicant answer that question?

A.    10

B.     20

C.     25

D.    32

Question 30)  In a different part of the form, the applicant is instructed to consider the Computer Skills set and list the #1 and #2 software in which he is most proficient. How many different ways can a random applicant answer this question?

A.    6

B.     8

C.     12

D.    16

Use the following data for problems 31 to 33.

At Dan's Super Deal used car dealership they have collected the following data showing the probability of selling 0 to 5 used cars each day.

Number of cars sold	Probability
0	.05
1	.05
2	.1
3	.2
4	.4
5	.2

Question 31)  What is the expected number of cars sold each day? Select the answer closest to your computation.

A.    2.50

B.     3.45

C.     0.17

D.    4.00

Question 32)  What is the probability that Dan's will sell at least 3 cars on a randomly selected day? Select the answer closest to your computation.

A.    0.80

B.     0.60

C.     0.40

D.    0.20

Question 33)  What is the standard deviation for the number of cars sold each day? Select the answer closest to your computation.

A.    2.50

B.     1.75

C.     1.87

D.    1.32

Use the following information to answer Q34 - Q37.

The HR department at a company has established that the probability an intern is offered a permanent position is 0.65. Eight interns startin the fall semester. Assume binomial distribution.

Question 34)  How many of those interns do you expect to be offered a full time position?

A.    6

B.     8

C.     5.2

D.    2.8

 

Question 35) What is the probability that no more than 5 interns are offered full time positions? Select the answer closest to your computation.

A.    0.2786

B.     0.5722

C.     0.7064

D.    0.4278

Question 36) What is the probability that 4 interns are offered a full time position? Select the answer closest to your computation.

1. 0.1875
2. 0.2936
3. 0.5000
4. 0.6500

Question 37) What is the probability that 2 interns are NOT offered a full time position? Select the answer closest to your computation.

A.    0.0217

B.     0.0253

C.     0.9783

D.    0.2587

Question 38) Customers join the waiting line of a post office at average rate of 3 customers per minute.  What is the probability of exactly 6 customers arriving into the post office within the next twominutes? Select the answer closest to your computation.

A.    0.2240

B.     0.1606

C.     0.0984

D.    0.0194

Question 39)  Average number of students asking for help at the library circulation desk is five per minute.  What is the probability of at least 4 students asking questions within the next minute? Select the answer closest to your computation.

A.    0.7350

B.     0.5595

C.     0.2340

D.    0.1754

Question 40)  This is Sam's senior year at college and he is sending applications to potential employers.  There is a3% chance for each application to get a job offer.  Sam has already sent 85 applications.  What is the probability of receiving at least 4 job offers? Select the answer closest to your computation.

1. 0.54
2. 0.25
3. 0.12
4. 0.02

Use the following data for problems 41 to 45.

The average finishing time at the 2013 Northshore inline marathon was approximately 2 hours and 24 minutes.  The standard deviation was approximately 32.5 minutes.  Assume the finishing times are normally distributed.

Question 41)  If a skater wants to finish in the top 10% of the fastest times, what time does the skater need?

A.    102.4 minutes

B.     190.3 minutes

C.     176.5 minutes

D.    210.4 minutes

Question 42) What is the probability of finishing in less than 1 hour and 50 minutes?

A.    0.18

B.     0.15

C.     0.85

D.    0.72

Question 43)  What is the probability of finishing in exactly 144 minutes?

A.    0.50

B.     0.67

C.     0.15

D.    0.00

Question 44)  If Jennifer finishes in 2 hours and 1100 skaters were in the race approximately, what place did Jennifer get in the race?

A.    253^rd place

B.     302^nd place

C.     178^th place

D.    Can't determine from the information provided

Question 45)  What is the probability of finishing in more than 2 hours and 15 minutes?

A.    0.84

B.     0.61

C.     0.58

D.    0.39

Use the following data for problems 46 and 47

While play is going on in a football game customers arrive at the hotdog stand on average every 3 minutes.  Assume the arrival time follows the exponential distribution.

Question 46)  What is the probability that the next customer will arrive within the 2 minutes?

A.    0.48

B.     0.25

C.     0.52

D.    0.85

Question 47)  What is the probability that the next customer will arrive in between 1 and 3 minutes?

A.    0.28

B.     0.65

C.     0.62

D.    0.35

Use the following data for problems 48, 49 and 50

Finish times at the Rollin on the River inline marathon follow a uniform distribution between 1 hour 18 minutes and 3 hours 12 minutes.

Question 48)  What is the mean completion time?

A.    2  hours

B.     2 hours 42 minutes

C.     2 hours 15 minutes

D.    1 hours 48 minutes

Question 49)  What is the probability of finishing the race in less than 2 hours 5 minutes?

A.    1.00

B.     0.61

C.     0.59

D.    0.41

Question 50)  What is the probability of finishing the race between 1 hour 52 minutes and 2 hours 22 minutes?

A.    0.26

B.     0.00

C.     0.74

D.    0.39