Reference no: EM133124111

CSC 420 Theory of Computation - University of Tabuk

Part 1:

Question 1: Give the following DFAs over ∑ = {a, b}

DFAs recognizes language L1 = L(M1)

DFA1 M₁ for L1

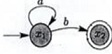
a) Construct a DFA for the language L1*.

b) What is the regular expression (RE) for L1?

Question 2: a) Consider the following NFA-ε over ∑ = {a, b}:

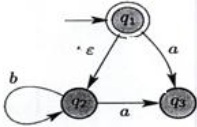
Convert this NFA-ε into DEA.

b) Build NFA for L((ba) U(ab)* over ∑ = (a, b).

Question 3: a) Consider the following CFG:

S→aS|aX|a

X→anX|bS|aa

1) What is the regular expression (RE) accepted by this CFG?

2) Show that whether this CFG is ambiguous or not:

3) Show that whether the word "abaaa" is accepted or not by this CFG:

b) Considering the below PDA, give the (state; stack) evolution of input string w = abb.

Question 4: Convert the following CFG into an equivalent CFG in Chomsky Normal Form(CNF) over the

∑ = {a, b}

S → aS|abX

X → baY

Y → aaX|ε