Construct a cumulative frequency plot

Reference no: EM131216922

Q1. State the complement of each of the following sets:

(a) Engineers with less than 36 months of full-time employment.

(b) Samples of cement blocks with compressive strength less than 6000 kilograms per square centimeter.

(d) Cholesterol levels that measure greater than 180 and less than 220.

Q2. Suppose that an ink cartridge is classified as being overfilled, medium filled, or underfilled with a probability of 0.40, 0.45, and 0.15, respectively.

(a) What is the probability that a cartridge is classified as not underfilled?

(b) What is the probability that a cartridge is either overfilled or underfilled?

Q3. Let X denotes the number of patients who suffer an infection within a floor of a hospital per month with the following probabilities:

x	0	1	2	3
P(X = x)	0.7	0.15	0.1	0.05

Determine the following probabilities:

(a) Less than one infection

(b) More than three infections

(d) No infections

Q4. Suppose that f(x) = 1.5x² for -1 < x < 1 and f(x) = 0 otherwise. Determine the following probabilities.

(a) P(0 < X)

(b) P(0.5 < X)

(d) P(X < -2)

(e) PAX < 0 or X > -0.5)

(f) Determine x such that P(x < X) = 0.05.

Q5. The thickness measurement of a wall of plastic tubing, in millimeters, varies according to a cumulative distribution function

Determine the following.

(a) P(X ≤ 2.0080)

(b) P(X > 2.0055)

(c) If the specification for the tubing requires that the thickness measurement be between 2.0090 and 2.0100 millimeters, what is the probability that a single measurement will indicate conformance to the specification?

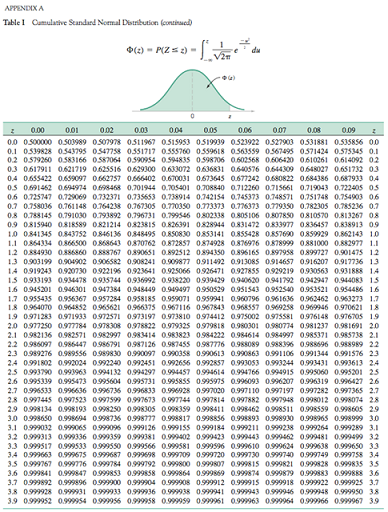
Q6. Use Appendix A Table I to determine the following probabilities for the standard normal random variable Z.

(a) P(- 1 < Z < 1)

(b) P(-2 < Z < 2)

(d) P(Z < -3)

Q7. The reaction time of a driver to visual stimulus is normally distributed with a mean of 0.4 second and a standard deviation of 0.03 second.

(a) What is the probability that a reaction requires more than 0.5 second?

(b) What is the probability that a reaction requires between 0.4 and 0.5 second?

Q8. The life of a semiconductor laser at a constant power is normally distributed with a mean of 7000 hours arid a standard deviation of 600 hours.

(a) What is the probability that a laser fails before 50150 hours?

(b) What is the life in hours that 95% of the lasers exceed?

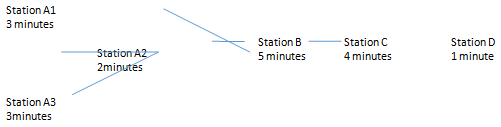
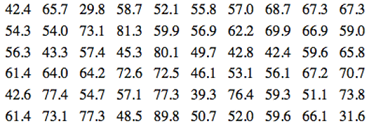
Q9. An important quality characteristic of water is the concentration of suspended solid material. Following are 60 measurements on suspended solids from a certain lake. Construct a stein-and-leaf diagram for these data and comment on any important features that you notice.

Q10. Construct a cumulative frequency plot and histogram for the weld strength data from Question 11.

(a) Use 8 bins.

(b) Use 16 bins and compare with part (a).

Q11. The shear strengths of 100 spot welds in a union alloy follow. Construct a stern-and-leaf diagram for the weld strength data and comment on any important features that you notice.

Construct a stem-and-leaf display for these data.

Q12. The following information on structural defects in automobile doors is obtained: dents, 4 pits, 4; parts assembled out of sequence, 6; parts undertrimmed, 21; missing holes/slots, 8; parts not lubricated, 5; parts out of contour, 30; and parts not debarred, 3. Construct and interpret a Pareto chart.

Q13. Eighteen measurements of the disbursement rate (in cm³/sec) of a chemical disbursement system are recorded and sorted:

6.50 6.77 6.91 7.38 7.64 7.74 7.90 7.91 8.21

8.26 8.30 8.31 8.42 8.53 8.55 9.04 9.33 9.36

(a) Compute the sample mean and sample variance.

(b) Find the sample upper and lower quartiles.

(d) Construct a box plot of the data.

(e) Find the 5th and 95th percentiles of the inside diameter.

Q14. The following table shows U.S. petroleum imports, imports as a percentage of total, and Persian Gulf imports as a percentage of all imports by year since 1973 (source: U.S. Department of Energy Web site https://www.eia.doe.gov/). Construct and interpret either a digidot plot or a marginal plot) or a separate stem-and-leaf and time series plot for each column of data.

Year	Petroleum Imports (thousand barrels per day)	Total Petroleum Imports as Percent of Petroleum Products Supplied (percent)	Petroleum Imports from Persian Gulf as Percent of Total Petroleum Imports (percent)
1973	6256	36.1	13.5
1974	6112	36.7	17.0
1975	6055	37.1	19.2
1976	7313	41.8	25.1
1977	8807	47.7	27.8
1978	8363	44.3	26.5
1979	8456	45.6	24.4
1980	6909	40.5	21.9
1981	5996	37.3	20.3
1982	5113	33.4	13.6
1983	5051	33.1	8.7

Q15. To investigate fuel efficiency, the following data were collected.

MPG, y	Weight, x₁	Horsepower, x₂	MPG, y	Weight, x₁	Horsepower, x₂
29.25	2464	130	17.00	4024	394
21.00	3942	235	17.00	3495	294
32.00	2604	110	18.50	4300	362
21.25	3241	260	16.00	4455	389
26.50	3283	200	10.50	3726	485
23.00	2809	240	12.50	3522	550

(a) Create two scatter diagrams of the data. What do you anticipate will be the sign of each sample correlation coefficient?

(b) Compute and interpret the two sample correlation coefficients.

Reference no: EM131216922

Questions Cloud

Calculate the weighted average cost of capital : Calculate the weighted average cost of capital (WACC) for Qantas - For the year ended June 2016 Qantas paid more than $500m to buy back shares. Explain possible reasons for Qantas to follow such a course of action?

Regarding its assets-liabilities and stockholders equity : Bravo Company has the following information regarding its assets, liabilities and stockholders' equity: Accounts Receivable $800, Equipment $10,000, Stockholders' Equity $7,700, Supplies $400, Accounts Payable $1,600, Bank Loan $4,200 and Tools $300...

What would you note from this negotiation : Discuss your negotiation-what went well? What did not? Was the outcome satisfactory? What about the process? If you were maintaining a lifetime negotiation journal, what would you note from this negotiation? What ethical issues arose? Would you li..

Type of artificial intelligence system : What type of artificial intelligence system is Watson considered to be? Justify your answer. What was the critical element that helped Watson finally reach the needed milestone?

Construct a cumulative frequency plot : Construct a cumulative frequency plot and histogram for the weld strength data from Question 11. Use 8 bins

Customers the responsibility of marketing : Is the functional operational strategy of finding more customers the responsibility of marketing, human resources, operations, or finance?

Identify some of benefits and some of costs to host country : Identify some of the benefits and some of the costs to the host country from allowing a multinational corporation to locate in a country with a developing economy.

Regarding its assets-liabilities and stockholders equity : Bravo Company has the following information regarding its assets, liabilities and stockholders' equity: Accounts Receivable $1,800, Prepaid Rent $2,000, Equipment $10,000, Stockholders' Equity $9,800, Supplies $400, Bank Loan $2,400 and Tools $300. D..

Determine motivation in organizations : What are three major characteristics that determine motivation in organizations? What are some of the variables within each?

User Account

All Pages