Reference no: EM13747
In this project we will consider the control of a synchronous generator supplying electricity to the grid. We will focus on the problem of frequency stability. The frequency at which the generator rotates is directly proportional to the frequency of the currents and voltages in the power grid. Hence, keeping the rotational frequency constant is of fundamental importance to the correct operation of the grid. A simpli�ed model to study the stability of a single generator connected to the grid is the so called swing equation given by:
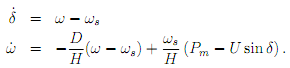
In this model ωs is the synchronous rotational velocity 2�Π50 rad/s. The constant D = 5 represents the damping induced by mechanical and electrical losses and the constant H has the value 4. The term Pm = 1/2 represents the mechanical power that is transformed by the generator into electrical power and the term Usinδ represents the electrical power and describes the e�ect the grid has on the generator. We will take U as the input since we can change its value by the voltage across the excitation coil in the generator's rotor.
A synchronous generator, when operating in steady state, maintains a constant angular velocity achieved by matching the supplied mechanical power Pm with the power lost through dissipation -D/H(ω - ωs) and the electrical power Usinδ �. When a fault occurs and a transmission line is tripped (opened) there is a sudden change in the electrical power and some generators will accelerate while other generators will decelerate. Once the fault is cleared and the transmission line is re-closed, di�erent generators will be rotating at di�erent angular velocities and voltages and currents in the power grid will no longer be sinusoids with a frequency of 50 Hz.
The objective of this project is to design a controller that will resume the steady state operation of the generator at 50 Hz. Please justify all your answers including relevant plots if necessary.
Attach the Simulink diagram to your report.
1. For which values of U and � is the pair ((�δ; ωs); U) an equilibrium point?
2. Linearize the swing equations around an equilibrium point.
3. Compute the transfer function from the input U to the output ω.
4. For which equilibria is the linearizes system stable?
5. Using the equilibrium point ((�Π/6; ωs); 1), simulate the linearized system and the non-linear swing equations for di�erent initial conditions. Comment on what you observe.
6. When a fault occurs in a transmission line the generator will either accelerate or decelerate. We will simulate this by using the initial value for ω to be 1% higher than ωs.
7. Design a controller to reduce by 50% the time to reach the equilibrium (under the initial conditions of the previous question). Show a plot of the evolution of the system when using the designed controller.
8. Keep increasing the value of ω until the system (swing equation+controller) becomes unstable. Compare with what happens when you do not use a controller.
9. Redesign your controller so that it stabilizes the angular velocity under faults that change the initial value of ω no more than 10% of its equilibrium value. Illustrate the operation of your controller with the relevant plots.