Reference no: EM1367620
1. Consider the following network example. With the indicated link costs along each link in the figure, use Dijkstra's shortest-path algorithm to compute the shortest path from x to all network nodes. Show how the algorithm works by computing a table.
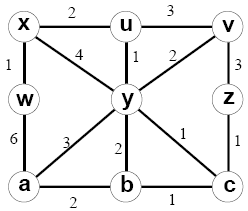
Answer: Let N' denote the set of nodes whose distance have been known so far, D(s) be the distance to a node s, and p(s) be the parent node of the node s on the shortest path from s to node x. We then construct the following table.
2. Consider the following network example. Suppose that the distance vector (DV) routing algorithm is used to compute the distance between nodes.
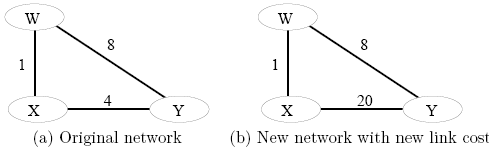
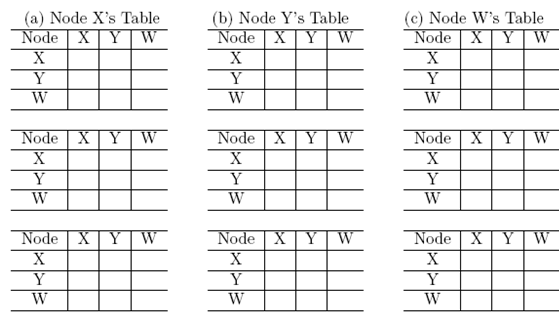
(a) Show the procedure of nodes X, Y and W computes their Distance Vector for network illustrated by Figure (a), i.e., link costs are C(xw)=1, C(xy)=4, and C(yw)=8.
Answer: In the following, each column shows the node X, Y and Z's table update respectively:
(b) Assume that after the DV is computed by all nodes, the link cost of xy changed from 4 to 20. Show the procedure of nodes X, Y and W updates their Distance Vector for network illustrated by Figure (b), i.e., link costs are C(xw)=1, C(xy)=20, and C(yw)=8.
Answer: In the following, each column shows the node X, Y and Z's table update respectively:
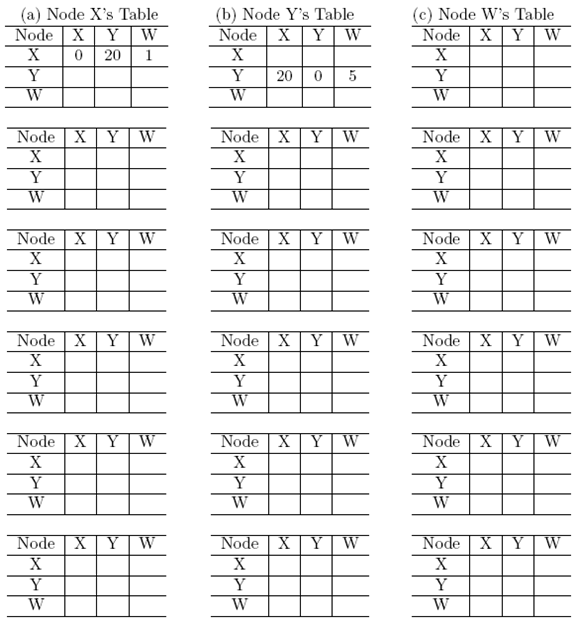
* If not enough, add more tables by yourself
3. We studied Dijkstra's link-state routing algorithm for computing the unicast paths that are individually the shortest paths from the source to all destinations. The union of these paths might be thought of as forming a shortest path tree. If each links has an associated cost and the cost of a tree is the sum of the link costs, then a spanning tree whose cost is the minimum of all of the spanning trees is called a minimum spanning tree. Both shortest path tree and minimum-spanning tree can be used for broadcast routing. By constructing a counterexample, show that the least-cost path tree is not always the same as a minimum spanning tree.
|
Write a program that exploit string library functions
: Write a program that exploit string library functions to do the following: -prompt the user to enter his name (of four parts) -count the number of characters in his name (excluding the white spaces).
|
|
Conclude what factors drive its demand for mba student
: Assume MTSU is attempting to conclude what factors drive its demand for MBA student credit hours (dependent variable). Information is available on following independent variables:
|
|
Argue that the problem is np complete
: Argue that the following prob is NP Complete. Given list of positive integers, u1,u2,...un (in binary representation) and asked if there is partition of this set into 3 subsets, each of which has same sum.
|
|
Calculating the forward rate
: Corporation A, a low rated company, desires a fixed-rate, long term loan. A currently has access to floating interest rate amount at a margin of 1.5 percent over LIBOR.
|
|
Compute the shortest path
: Use Dijkstra's shortest-path algorithm to compute the shortest path from x to all network nodes - computes their Distance Vector for network
|
|
Estimate cost elasticity of demand for education
: Estimate cost elasticity of demand for education at this university. Is cost elasticity of demand for university tuition elastic or inelastic according to answer in part (i) Why.
|
|
How much time is necessary for a particle of string
: A Carnot engine performs work at the rate of 380 kW when using 730 kcal of heat per second. If the temperature of the heat source is 560 C, at what temperature is the waste heat exhausted.
|
|
Which airline has lower costs
: If Fly Right were to go out of business, it would be able to rent its plane to another airline for $30,000. Which airline has lower costs.
|
|
Where on the y axis is total electric field zero
: A model rocket rises with constant acceleration to the height of 3.7, at which point its speed is 25. what was the magnitude of the rocket's acceleration.
|