Reference no: EM13256604

1. Simulate 2000 coin flip experiments with a biased coin with "success" probability (chance of 1) p = 1/5. Plot an outcome of the proportion of successes with respect to the number of coin flips. Supply your code.

2. Simulate the total number of trials required to achieve rst success, where success is rolling a pair of twelves on two fair twelve-sided die. Repeat this experiment 50000 times, and calculate the sample mean and sample standard deviation over these 50000 trials. Supply your code.

3. Simulate 3000 coin flip experiments with a biased coin with "success" probability (chance of 1) p = 7/8. Repeat this experiment 1000 times, and plot the overall average proportion of successes with respect to the number of coin flips, together with the maximum and minimum proportion of successes over these 1000 repeated experiments. Supply your code.

4. Using the inverse-transform method on uniform (0, 1) (pseudo)random variates, simulate one million outcomes from X ∼ Exp(3), and compute the sample mean and sample variance of the indicator I_{X>3} of the rare event l = P(X > 3). The sample mean is called the crude Monte Carlo estimator.

5. Using the inverse-transform method on uniform (0, 1) (pseudo) random variates, simulate one million outcomes from Y with Cauchy pdf f(y, μ, τ) =  τ ( Π ( τ² +( y - μ)²))^-1, with μ = 3 + 1/6 and τ = 1/6, and compute the sample mean and sample variance of

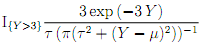
The sample mean is called a likelihood ratio estimator of the rare event l = P(X > 3), with X ∼ Exp(3). Supply your code.

6. Using the inverse-transform method on uniform (0, 1) (pseudo)random variates, simulate one million outcomes from Z with Cauchy pdf f(z, μ, τ) =  τ ( Π ( τ² +( z - μ)²))^-1, with μ ranging over {3:00, 3:05, : : : , 3:50} and τ ranging over {0:10, 0:11, : : : , 0:50}.

Plot (over the two-dimensional range of ( μ, τ)) the sample mean and sample variance of

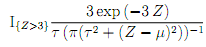
Comment on the "best" value for the parameter pair ( μ, τ). Supply your code.