Reference no: EM1379025
1.Use the second-order accurate central difference approximation and the first-order forward difference approximation to evaluate δ(e-2x)/δx at x = 1. A step size of Dx = 0.1 is to be used. Compare this to the actual value of the derivative and compute the percent error for each approximation defined by
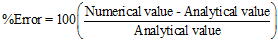
2. Consider the three-dimensional heat conduction equation
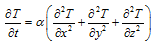
Obtain an explicit finite difference equation using first-order forward time and second-order central spatial differencing. You do not have to derive the difference approximations; simply use them.
3. Consider a fluid bounded by two parallel plates extended to infinity such that no end effects are encountered. The walls and the fluid are initially at rest. The lower wall is suddenly accelerated in the x-direction. The coordinate system is such that the lower wall coincides with the xz-plane to which the y-axis is perpendicular. The spacing between the two plates is denoted by h.
The equation for this problem is
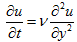
where n is the kinematic viscosity of the fluid. It is required to compute the velocity profile u = u(y,t). The problem has the following initial and boundary conditions
Initial Condition:
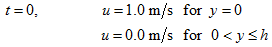
Boundary Condition:
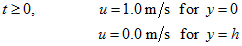
The fluid has a kinematic viscosity of 0.000217 m2/s and h = 40 mm. Your solution should be run until t = 1.08 seconds. Various time steps are to be used to investigate the numerical schemes and the effect of the time step on stability and accuracy.
Write a code (or multiple codes) to solve this problem for the following schemes and conditions.
a) FTCS Explicit with time steps 0.002 and 0.00233 sec
c) FTCS Implicit with time steps 0.002 and 0.01 sec
If j = 1 at the lower surface and a step size of Dy = 0.001 m is used, then j at the upper surface will be 41. Note that n = 1 corresponds to t = 0.
For each case of each method, plot the velocity profile for four difference times on the same graph: 0.27 sec, 0.54 sec, 0.81sec and 1.08 sec. (You will have 4 plots in all, each with four curves.) Remember to use proper plotting techniques, including title, axis labels, units, legend, and legibility. Submit your plots in hardcopy, and a copy of your code both in hardcopy and electronically on Canvas.
|
Decimal octal hex binary value
: Decimal Octal Hex Binary Value The table depicts device control codes from the ____character coding standard.
|
|
Formal software development approaches
: An aspect of the preferred procedure for almost all formal software development approaches is to do some design before coding.
|
|
Naming conventions in programming language
: Discuss and explain why naming conventions are important and why programmers should consistently follow them. Include in this discussion problems that could arise in naming variables if one convention is not followed.
|
|
Introduction to the theory of computation
: The language define through the equality of two 2DIM-DFA machines on all inputs is un-decidable. The full definition of 2DIM-DFA can be discovered in Sipser's Introduction to the Theory of Computation.
|
|
Compute the percent error for each approximation
: Compare this to the actual value of the derivative and compute the percent error for each approximation
|
|
Advantage of oo development
: An advantage of OO development is consistency of language and OO development often omits writing a distinct requirements specification document.
|
|
Implementing reusable code
: Many programming languages exist in various libraries and on the Internet and using some of these functions and process, this can permit you to use these technique rather than having to write out the code from scratch on your own.
|
|
Creating an idef1x e-r diagram
: The scenario is that the Public Affairs Office at Highline University gets requests for speakers on particular topics. To be able to respond to such request, that office wishes to create a database.
|
|
Difference between encapsulation and information hiding
: Discuss and explain the difference between encapsulation and information hiding. In addition, describe the role both of these concepts play in helping to make designs more robust and extensible.
|