Reference no: EM13137232

1. [CAPM Numerical Exercise] Consider the following three assets:

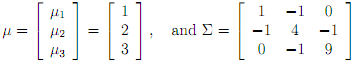
Write a computer program (for example, using Matlab) to answer the following questions:

(i) Plot the ecient frontier for μP ∈ [0; 6]. That is, trace out in (σP ; μP )-space the locus of minimum variance portfolios made up of these three assets subject to w>

P  = P for each P in a grid over the interval [0; 6].

(ii) What are the portfolio weights, wMV P , of the minimum variance portfolio?

(iii) Suppose we add another asset that pays a risk free return of rf = 1:1. Plot the new ecient frontier together with the ecient frontier from part (i).

(iv) What is the tangency portfolio, wT ? What is the mean return and standard deviation of the tangency portfolio, μT and σT ?

(v) Verify that the Sharpe ratio for an investor that chooses an ecient portfolio is higher than the Sharpe ratio for an investor that ignorantly chooses to invest equal amounts in the three risky assets.

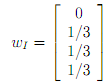
(vi) What are the market betas for the three risky assets? Interpret.

2. [General Equilibrium and Uncertainty with Incomplete Markets] Consider a two-period exchange economy with two agents. They have identical utility functions:

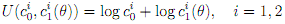
Where c0 is agent i's consumption level at date 0, and ci () is agent i's consumption level at date 1 if state  occurs. There are two equally likely states at date 1. Consider the following endowment structure:

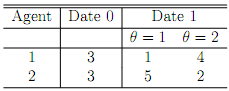
(i) Describe the Pareto optimum or set of Pareto optima. Is it unique? Is perfect risk sharing achieved? Explain. Describe how the risk sharing arrangement would change if agent 1's period 1 endowment in state  = 2 was some x > 4?

(ii) Suppose only non-contingent claims can be traded (i.e., a claim to one unit of consumption for sure to be delivered at date 1). Show that an equilibrium allocation cannot be Pareto optimal. [Hint: You do not have to solve for the equilibrium.

(iii) Suppose instead that in addition to the non-contingent claim, there is a second security that pays z units of the consumption good in state  = 1, and zero otherwise. Describe the equilibrium. Is the allocation Pareto ecient? Explain.

(iv) Solve for the Arrow-Debreu competitive equilibrium. What is the relationship between the prices of the Arrow-Debreu securities and the prices derived for the securities traded in part (iii).

3. [Innite Exchange Economy with Uncertainty] An economy consists of two innitely lived consumers named i = 1; 2. There is one nonstorable consumption good. Consumer i consumes t at time t. Consumer i's preferences over consumption streams
are represented by

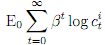
where  2 (0; 1). The endowments are decided each period by an unsophisticated and semi-barbaric king. At each date t, the king ips a fair coin. If the outcome of the coin toss is heads, consumer 1 receives one unit of the consumption good, and consumer 2 receives nothing. If the outcome is tails, consumer 2 receives one unit of the consumption good, and consumer 1 receives nothing.

(i) Let st 2 fH; Tg denote the state of the economy at date t. q0 t (st) denotes the time 0 price of an Arrow-Debreu security that pays one unit of consumption in date t conditional on state st, and ci t(st) denotes consumer i's consumption at date t in state st. Dene an Arrow-Debreu competitive equilibrium.

(ii) Compute the equilibrium under the assumption that Arrow-Debreu securities are traded in time 0 after the realization s0 = H.

(iii) Suppose that one of the consumers markets a derivative asset that promises to pay :05 units of consumption each period. What would the price of that asset be