Reference no: EM13328133

Part -1:

Question #1. Consider a sequence of non-zero real-numbers r1, r2,............rN such that no two numbers are equal. Using these numbers, we create an (N x N) square matrix R such that the (i, -j)-th element of R is given by

a_ij = a(i,j) = (i,j)-th element of R = rk,

where k = min(i,j), i = 1, 2, ..., N;j = 1, 2, ..., N. For example, min(2, 5) = 2. Similarly, min(78, 49) = 49 => a(78, 49) = r49. In general

aij = a(i,j)= (0)-th element of R = r₂ k = min(i, j).

In other words, given i and j, find k first, and then find a(i,j) = rt.

A. Write the elements of matrix R in terms of real-numbers r1, r2,..............rN. Clearly, show at least the top 4 x 4 part and all the elements on the four corners.

B. Is this a symmetric matrix?

C. Carry out appropriate EROs to reduce the matrix R to its echlon form.

D. Carry out appropriate EROs to reduce the matrix R to its row echlon form.

E. Carry out appropriate EROs to reduce the matrix R to its reduced row echlon form.

F. It is claimed that a unique solution always exists for the linear system Ri = b. Do you agree? Give justification.

G. Solve the system when N = 10. rk = k. k = 1, 2, ..., 10, and b = [1 1 1 ... I ]^T.

HINT: We introduced four technical words: 'forward', 'elimination', 'backward', 'substitution'. See if a mix of these will be useful here.

Part -2:

Question #1. A matrix A is known as a circular matrix if its 2na row is obtained by circularly shifting the lsi row. Same way 3P¹ row is obtained from rd row and so on. Consider the following 3 x 3 circular matrices A and B:

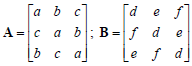
I Show tha C = A B is also a circular matrix.

IL Without computing D, show that D=ABB-B=AB²¹ is also a circular matrix. Justify.

III.Show that the vectors

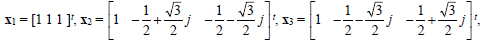
satisfy the linear systems: A x1= λ1x1, Ax2= λ2x2, A x3= λ3x3. Here, j = √-1

IV. For the three vectors in Part 11, find the corresponding values of λ₁, λ₂, and λ₃.

V. Compute the determinant of A.

VI. Create a 3 x 3 matrix X where x₁ is 1^st column, x₂ is 2^nd column & x₃ is 3^rd column.

VII. Compute A^-1 Is A^-1 circular?

VIII.  It is known that we can write A = X A X^-1, where A is a 3 x 3 diagonal matrix having Xi, X2, and A3 on its main diagonal. Using the expression A = X A X^-1, find a matrix E such that A² = X E

IX. Given that first row of a 4 x 4 circular matrix A is [4 3 2 1], write the matrix A.

Part -3:

Question #1. Find the perpendicular distance of the plane 5 x + 2 y - z = -22 from origin 0 by first finding the co-ordinates of the point P on the plane such that OP is perpendicular to the given plane.

Question #2. We have an empty cardboard box of dimensions breadth = 4 az length = 5 in, and height = 6 m. An ant and a fly are sitting at one of the 8 comers inside the box and wish to go get some food at the corner diagonally across (the farthest point in the box for them). What is the minimum distance the ant must travel before it gets to the food? How about the fly?

Question #3. Let N = 3 and M = 2N. M-th root of 1 is given by ω =-α, where α =exg[2Πj/N] j = √-1. It is verified as

 ω^M = ω^2N= (-α)2N = (-1)^2N exp[-4Πj] = cos4Π -j sin4Π = 1.

Note that (-1)² = 1. Using this M-th root of 1, we create an (M xM) square matrix R. The (a. b)-th element of R is given by

r_ab= ω^(a-1)(b-1 a = 1,2,........m b = 1,2..........m 

A. Write the matrix R expressing its elements in terms of α. Show at least the top 3 x 3 part and all the elements on the four corners. Is R a Hermitian matrix?

B. Consider another (M x M) square matrix S such that the (c, d)-th element of S is given by

s_c,d =ω^(c-1)(d-1) c =1, 2, ...,M; d =1,Z ...,M

Let T = SR Write the elements of T. Compute determinant of T.

C It is claimed that inverse of S, S^-1 = (1/M)R It Is that correct? Express R^-1 in terms of S. Justify.

D. Find the rank of the matrix S and its nullity. Are all the rows of S Li?

E. Solve the linear system Rx = b for M= 6 and b = [1 1 1 1 1 l]^t.

You may find these very useful:

exp[ja] = cosα +j sinα;                     1+α+α² ...+α^M-1= [1-α^M]/(1-α).