Reference no: EM1383841

You are expected to complete a project related to inferential statistics. The project must contain the following components

a. Title of the project
b. Introduction and Objectives
c. Data collection: Data should be a real a data set (you may find the data in the internet, published papers but please provide the source).
d. Display the data graphically (if you wish)
e. Compute all relevant summary statistics.
f. Perform the inferential statistics (Interval estimation, Hypothesis testing etc.)
g. Conclusions
h. References

Many customers at a certain grocery store have been complaining about the amount of time they wait in line at the checkout stand (Albright 144). So the manager decides to offer a coupon to anyone who waits longer than a certain amount of minutes, say, 2.5 minutes. Before starting the program, she wants to find the probability that a randomly selected customer will receive a coupon. If the random variable X denotes the time spent waiting in line, then the manager wants to know P(X > 2.5). She hypothesizes that because exponential distribution is used to describe the wait time between events, then X should be exponential. As said in Essentials of Mathematical Statistics, a random variable X has an exponential distribution if its probability density function is

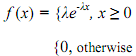
where λ = 1/β > 0, and when its cumulative distribution function is

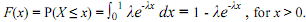
So, we must complete the following objectives:

1) Show that the random variable X is exponential.
2) Compute the probability of the wait time when it is greater than 2.5 [P(X > 2.5)].
3) Find the relevant summary statistics.

The Data Set

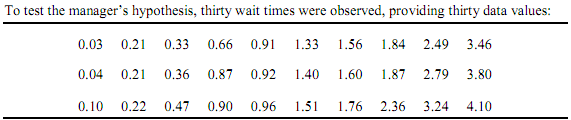
The Distribution

The chart below shows the frequency of the data set values on each interval, as well as the relative frequency. When the relative frequency is represented in a histogram, the histogram resembles the shape of a graph of an exponential pdf.

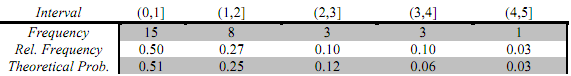
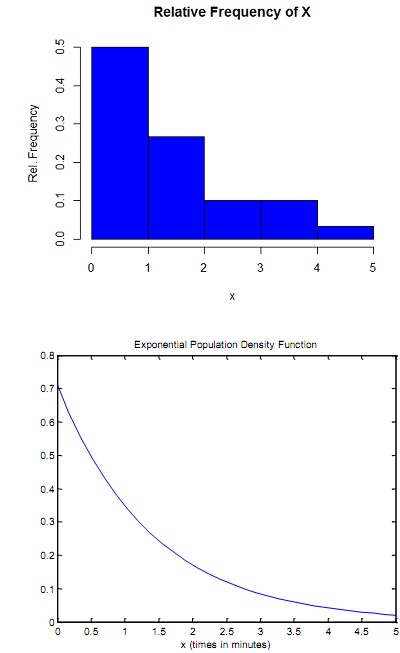
As shown above, both figures are practically alike. To further verify the hypothesis, the mean of X (the average wait time) is found to be 1.41 minutes. This means the parameter λ (1/mean) is approximately 0.71.

So if X is exponential with λ = 0.71, then, for instance,

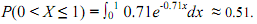
This means that if X is indeed exponential with λ = 0.71, then about 51% of observed values of X will be between 0 and 1 minute. Note how the relative frequencies and theoretical probabilities are very close in each case. This leads us to conclude that the hypothesis of X being exponential with parameter λ = 0.71 is reasonable.

Thus the probability that a randomly selected customer will receive a coupon is

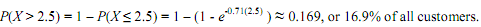
Summary Statistics

Conclusion

All-in-all, it can be proven that a random variable does have an exponential distribution from its data set. Note how the expected value, standard deviation, and mean are the same value. That is another property of exponential distribution, which is more evidence towards that distribution.