Reference no: EM133776533

Algorithms Assignment:

Learning Outcome 1:  Apply specific search algorithms studied in the course to slightly unfamiliar problems.
Learning Outcome 2: Select appropriate data structures to optimize the performance of the search algorithms.
Learning Outcome 3: Measure and compare the solution quality and time and memory used by algorithms.

General Instructions
Programming Language: All students are required to use the Java programming lan- guage for this assignment. You may only use in-built Java library methods and classes (that are listed in the documentation for the Java Standard Edition API), as well as ones you write yourself. You are not permitted to import any third-party libraries to use in this assignment.

Individual Assignment: Each student must complete the main tasks specified as an indi- vidual to demonstrate achievement of the learning outcomes; no collaboration is permitted.

Marking Guideline: Marks are provided for functionality and for efficiency (optimising the execution times of your algorithms). The purpose of these tasks is three-fold: (i) you need to problem-solve: figure out how best to solve each task, (ii) implement and test the solution, and
(iii) measure execution time and/or memory needed for the algorithms to solve the problems.

Getting Started
Download the package assignment2base.zip from Canvas. In this package you will find three files:
UpgradeCheck.jar: A pre-compiled Java file that contains two classes: MapGenerator and
UpgradeCheck. These classes are black-boxes, you do not need to know how they work.
When compiling, you will need to ensure this jar file is on the Java classpath. You can use the -cp flag when invoking the Java compiler to set the classpath. For example:
javac -cp .;UpgradeCheck.jar *.java
This file was compiled with Java 21. To run it, you will need to use version 21 or higher.
UpgradeCalculator.java: This is where you will complete your assignment, some starting code has been provided to allow compilation.
UpgradeMain.java This is the main class to control the program, calling your methods from UpgradeCalculator.java. You may modify this file underneath the marked comment in order to test your code, but the modifications will not be really not part of the assignment.

Problem Scenario
Perhaps you remember the bustling metropolis of Veridian City in Assignment 1. The initial chaos of rush hour has been meticulously mapped and analysed. Thanks to your brilliant work as a digital traffic engineer, the city council now has a clear picture of the traffic bottlenecks and inefficiencies plaguing the streets. However, understanding the problem is only the first step. Your mission in Assignment 2 is to take your analysis to the next level. The city council is counting on you to design and propose real, actionable changes to the traffic system to solve the problems that have been identified. This involves tackling more complex problems and developing innovative solutions that go beyond basic analysis. Your task is to optimize traffic flow, reduce congestion, and improve overall commute times. The future of Veridian City's transportation network depends on your ability to think creatively and implement effective strategies. Every decision you make could lead to smoother commutes, lower emissions, and a happier, more efficient city.

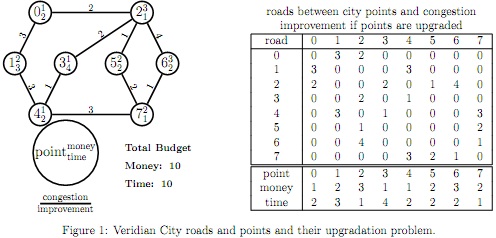
Figure 1 shows an example of a roadmap of a city like the Veridian city. In fact it is the test map given in UpgradeMain.java in the base code supplied to you. Note that in every run of your program, a map generated randomly by the MapGenerator class will be used. Also, note that the points or intersections are denoted by indexes 0, . . . , n - 1, the roads by a pair of end points
while the other values at the points and the roads in the map could have fractions.

Each city point or intersection in the map needs certain amount of money and length of time to upgrade the point with security cameras, traffic lights, and so on. If a point or intersection is upgraded, then all the roads incident on the point are basically covered and the congestion levels of the incident roads get improved with certain levels. To be more specific, the value of upgrading a point should be considered equal to the sum of the weights of the incident roads. Note that upgrading only one end point of a road is considered sufficient in this case to improve the congestion level of a road. So upgrading both end points will not make any difference from upgrading just either end. The city council has a maximum budget of the money and also a time limit on the upgradation tasks to be completed. Obviously, the city council wants to maximise the coverage of the roads in the city and thus reduce the congestion level. You have to find which city points are to be upgraded.

The above problem actually could be modelled using a two dimensional knapsack problem. Let mk and tk be the money and time needed for point k. The total money and the time available are M and T respectively. Let sk be a boolean variable to denote whether a city point is selected for upgradation. Also, let c(s, k) denote congestion improvement possible if point k is upgraded but clearly c(s, k) will depend on the selection of other points in s since a road might have been already covered by the other end point of the road. So mathematically, the problem is as follows:

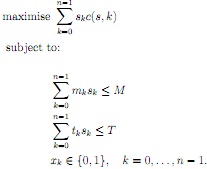
Problem Tasks

There are 4 tasks in this assignment. Three are to solve the problem using three methods such as dynamic program, heuristics, and metaheuristics. The other one is to report their performance.

The problem generator will give you the required arrays and the budgets as shown in Figure 1. You will use these as input in your solvers. The solvers will find the points to be upgraded, total congestion improvement that could be achieved, and total money and time to be spent. Also, determine the execution time and memory required by each solver to solve a given problem.

Dynamic Programming Solver: A method named dynamicProgrammingSolver is in the UpgradeCalculator.java. Write code inside that method to get a dynamic program- ming solver for the problema. Hint: use the example program for the dynamic programming
solver for the knapsack problem as a seed.

Heuristic Solver: Another method named heuristicSolver is also in the UpgradeCalculator.java. Write code inside that method to get a heuristic solver.

Hill Climbing Solver: Yet another method named hillClimbingSolver in the UpgradeCalculator.java. Write code inside that method to get a hill climbing metaheuristic solver for the problem. Hint: use the example program for the hill climbing solver for theknapsack problem as a seed.

Reporting Solver Performance: Generate 5 problems of different sizes using the problem generator given in the UpgradeCheck.jar file. Run each of the solver on the generated problems. The dynamic programmig solver would give the same solution every time you run the solver on the same problem and that is the optimum solution. The other two solvers may give different solutions in different runs, if randomised decisions have been made.In that case, run each solver on each problem at least three times and take the average to report the results. Include all the five instances in the report. Show all the results in tables or charts. Write a commentary on the solvers and compare their performance.

Task 1 Dynamic Programming Solver:
Correctly implements a dynamic programming algorithm to give an exact solution
Efficient implementation in time complexity
Efficient implementation in space complexity

Task 2 Heuristic Solver
Implementation of a heuristic algorithm
Selection of an appropriate heuristic
Quality of solution (exact solution not required, but the closer the better)
Efficient implementation in time complexity
Efficient implementation in space complexity

Task 3 Hill Climbing Solver:
Implementation of a hill climbing algorithm
Quality of solution (exact solution not required, but the closer the better)
Efficient implementation in time complexity
Efficient implementation in space complexity

Report:
Test data and results (five problems with three runs each on each solver)
Good discussion with comparison of solver performance.
Correct time complexity given for each algorithm with matching code provided
Correct space complexity given for each algorithm with matching code provided
Providing correct proofs and explanation.