Reference no: EM132979919
COMP30026 Models of Computation - University of Melbourne
Aims and Procedure
One aim of this assignment is to improve and test your understanding of propositional logic and first-order predicate logic, including their use in mechanised reasoning. A second aim is to develop your skills in analysis and formal reasoning about complex concepts, and to practise writing down formal arguments with clarity.
Challenge 1
As a blade runner, Rick Deckard's task is to identify replicants. These look exactly like humans, but they have in fact been manufactured in the labs of Tyrell Corporation. Some replicants are programmed to always speak the truth, while others are programmed to always lie. Unfortunately the same goes for the humans that Deckard deals with: some are always truthful, and the rest always lie. One day, Deckard interviewed two individuals, X and Y , who made these statements:
X: "Y is a truthful human"
Y : "X is a lying replicant"
Task 1A. Capture, as a single propositional formula, the information that was thereby available to Deckard. You will need to take into account who makes each statement. Use propositional
letters as follows:
P : X is truthful R: X is human
Q: Y is truthful S: Y is human
Task 1B. Deckard, a competent logician, realised that the two statements would not allow him to determine whether either was human or not. Determine which truth assignments to P , Q, R, S make your formula from Task 1A true.
Task 1C. Now, Deckard later found out, from a reliable source, whether Y was truthful or not, and based on that information, he knew exactly whether X was human and also whether Y was human. Given this information, determine, for each of X and Y , whether they are a human or a replicant.
Challenge 2
Conjunctive normal form (CNF) is an adequate representation of Boolean functions, because every Boolean function can be written as a conjunction of disjunctions or literals. The set {∧, ∨, ¬} suffices to write all possible Boolean functions, that is, that set of connectives is functionally complete. In fact, from De Morgan's laws we can conclude that {∧, ¬} is a functionally complete set of connectives, since P ∨ Q ≡ ¬(¬P ∧ ¬Q), so that disjunction can always be translated into negation and conjunction. Similarly {∨, ¬} is functionally complete.
Task 2. Show that {⇒, f } is functionally complete. That is, show that every propositional formula has a logically equivalent formula that uses only variables, the "if-then" connective, and the constant f (denoting "false"). We ask you to do this by writing a Haskell function that turns an arbitrary propositional formula into an equivalent one that uses only ⇒ and f (plus any parentheses or propositional letters you need).
Challenge 3
A 7-segment display is an arrangement of seven LEDs (labelled i-o), as shown here. Arrays of such displays are commonly used to display characters in remote controls, blood pressure monitors, dishwashers, and other devices. Each LED can be on or off, but in most applications, only a small number of on/off combinations are of interest (such as the 10 combinations that allow the display in a digit in the range 0-9). In that case, the display can be con- trolled through a small number of input wires. For example, four input wires provide 24 input combinations, enough to cover the ten different digits.
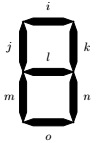
Here we are interested in using a 7-segment display for some uppercase letters. We want it to be able to show eight different letters, namely A, B, C, D, E, F , G, and H. For example, to show A, all the display segments, except o, should be lit up, giving the pattern . In detail, we want the eight different letters displayed as A,B, C, D, E, F, G, and H, respectively. Since there are eight letters, we need three input wires, modelled as propositional variables P , Q, and R. We will need to decide on a suitable encoding of the eight letters. One possibility is to let A correspond to input 000 (that is, P = Q = R = f ), B to 001 (that is, P = Q = f and R = t), and so on. If we do that, we can summarise the behaviour of each input combination in the table below:
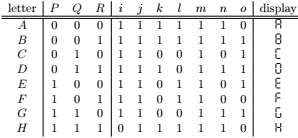
Each of the seven segments i-o can be considered a propositional function of the variables P , Q, and R. This kind of display can be physically implemented with logic circuitry, using circuits to implement a boolean function for each of the outputs. Here we assume that only three types of logic gates are available: An and-gate takes two inputs and produces, as output, the conjunction (∧) of the inputs. Similarly, an or-gate implements disjunction (∨). Finally, an inverter takes a single input and negates it (¬). We can specify such a circuit by writing down the Boolean equations for each of the outputs i-o. For example, segment i is turned off (is false) exactly when the input is 111. So, i can be captured as ¬P ∨ ¬Q ∨ ¬R.
For efficiency reasons, we often want the circuit to use as few gates as possible. For example, the above equation for i shows that we can implement this output using five gates. But i = ¬(P ∧Q∧R) is an equivalent implementation, using only three gates. Moreover, the seven functions might be able to share some circuitry. For example, if we have already implemented a sub-circuit defined by u = Q ∧ R (introducing u as a name for the sub-circuit), then we can define i = ¬(P ∧ u), and we may be able to re-use u while implementing the other outputs (rather than duplicating the same gates). In some cases it may even be feasible to design a circuit that is not minimal for a given function, but provides a minimal solution when all seven functions are designed.
Task 3. Design such a circuit, using as few gates as possible. You can define any number of sub-circuits to help you reduce the gate count (simply give each a name).
# An example of a set of equations in the correct format: i = -Q R + Q -R + P -Q -R
j = u + P (Q + R) k = P + -(Q R)
l = u + P i u = -P -Q
# u is an auxiliary function introduced to simplify j and l
Challenge 4
The logic of equality. Is it possible to assign values to the variables a, b, c, and d, so that the formula (a=b)∧(b=c)∧(c=d)∧¬(a=d) is true? How about the formula (a=c) ⇔ (¬(a=b)∨¬(b=c))? These are examples of satisfiability questions in the system of equality logic. A formula in equality logic includes a collection of variables, such as a, b, c, and d. These variables are related to one another by equalities, such as (a=b). Equalities are assembled into formulas using connectives, like the ones we are familiar with from propositional and predicate logic: ∧, ∨, ¬, ⇒, ⇔, and ⊕. An equality logic formula is satisfiable if there is some assignment of values to its variables that makes the formula evaluate to true, under the usual semantics of equality and the logical connectives.
Task overview. In this challenge, you will complete an implementation of a satisfiability decision procedure for equality logic formulas. The decision procedure will work as follows:
1. You will devise a way of modelling an equality logic formula as an equisatisfiable propositional logic formula, using the strategy below.
2. You will implement this modelling strategy as a Haskell function that translates equality logic formulas into propositional logic formulas, supported by some scaffolding code we provide. We break this step down into four implementation tasks, described below.
3. We provide a satisfiability algorithm for propositional logic, which will decide whether your propositional formula (and thus also the original equality logic formula) is satisfiable or not.
The strategy. The key to satisfying an equality logic formula in is knowing which variables to assign to the same values. If we know whether or not each pair of variables shares a value, we have all we need to evaluate the formula. If this information were to be encoded in propositional logic, what propositions might we use? To encode an equality logic formula in propositional logic is to use these propositions to capture the logical structure of the original formula, along with the special properties of the equality relation, in a single propositional formula. The four tasks below will guide you to capturing this strucure.
Task 4A. Using your propositional variables, implement a Haskell function to encode the logical constraints implied by an equality logic formula's connectives as a formula in propositional logic.
Task 4B. Equality is a reflexive relation: A variable always equals itself, so a formula like (a=a) is always true in equality logic. Using your propositional variables, implement a Haskell function to encode the constraints implied by this property as a formula in propositional logic.
Task 4C. Equality is also a symmetric relation: Equality can't be true in one ‘direction' and not the other. (a=b) and (b=a) are equivalent in equality logic. Using your propositional variables, implement a Haskell function to encode the constraints implied by this property as a formula in propositional logic. Hint: Depending on your propositional variables, this may be a short formula.
Task 4D. Finally, equality is a transitive relation: Equalities chain together. If we know (a=b) and (b=c), then we must have (a=c) too, even if this is not specified directly in an equality logic formula. Using your propositional variables, implement a Haskell function to encode the constraints implied by this property as a formula in propositional logic. Hint: For each individual group of three variables, consider all of the ways in which the transitive property could affect the formula.
Challenge 5
Consider the four first-order predicate formulas
F1 : ∃x (∃u (∀v (P (u, v, x))) ⇒ ∃y (Q(x, y))) G : F1 ⇒ F2
F2 : ∃x (∀v (∃u (P (u, v, x))) ⇒ ∃y (Q(x, y))) H : F2 ⇒ F1
Task 5A. Determine whether G is valid or not. Either provide a proof that uses resolution to show validity, or else specify an interpretation that makes G false.
Task 5B. Determine whether H is valid or not. Either provide a proof that uses resolution to show validity, or else specify an interpretation that makes H false.
Challenge 6
The notation we use for first-order predicate logic includes function symbols. This allows a very simple representation of the natural numbers. Namely, for natural numbers, we use terms built from a constant symbol (here we choose a, but any other symbol would do) and a function symbol of arity 1 (we will use s, for "successor"). The idea is that 0 is represented by a, 1 by s(a), 2 by s(s(a)), and so on. In general, s(x) represents the successor of x, that is, x+ 1. Logicians prefer this "successor" notation, because it uses so few symbols and supports recursive definition-a natural number is either ‘a' (the base case), or it is of the form ‘s(. . .)', where . . . is a term representing a natural number. (Of course, for practical use, we prefer the positional decimal system.)
With successor notation, we can capture the usual "less than or equal" ordering of N (the set of natural numbers) with these two axioms, where L(x, y) stands for x ≤ y:
∀y(L(a, y))
∀x∀y(L(x, y) ⇒ L(s(x), s(y)))
(1) says that 0 is smaller than or equal to any natural number, and (2) says that if x ≤ y then x + 1 ≤ y + 1. Similarly, we can capture addition by introducing a predicate symbol for the addition relation, letting P (x, y, z) stand for x + y = z:
∀y(P (a, y, y))
∀x∀y∀z(P (x, y, z) ⇒ P (s(x), y, s(z)))
Turning the conjunction of (1)-(4) into clausal form, we end up with this set of clauses:
{{L(s(v1), s(v2)), ¬L(v1, v2)}, {L(a, v3)}, {P (s(v4), v5, s(v6)), ¬P (v4, v5, v6)}, {P (a, v7, v7)}}
Task 6A. Use resolution to show that
∃x∃y(L(s(a), x) ∧ P (y, y, x)) (5)
is a logical consequence of the axioms (1)-(4).
Task 6B. Your resolution proof will not only establish the truth of (5). The resolution proof provides a sequence of most general unifiers, one per resolution step, and when these are composed, in the order they were generated, you have a substitution that solves the constraint 1 ≤ x∧y+y = x. Give that substitution and explain what it means in terms of natural numbers.
Attachment:- Models of Computation.rar