Reference no: EM133006890

COMP2230 Algorithms - The University of Newcastle

Problem Overview

This assignment can be done individually or in pairs and it involves performing two or four tasks, respectively.

1. Write a program that generates a random maze of a requested size.
2. Write a program that implements DFS technique for solving a maze.
3. Pairs only: Write a program that implements BFS technique for solving a maze.
4. Pairs only: Compare and contrast the two techniques on the basis of program running time, and the number of ‘steps' taken to solve the maze.

We will now look at how to define our maze, before describing each task in more detail.

Maze Definition

Your aim is to create a simple maze that will have exactly one path from any point in the maze to any other point (as an example, see Figure 1). Therefore, your maze will not have inaccessible areas (cells without any missing walls around them), open areas (cells without walls), and no circular paths (loops).

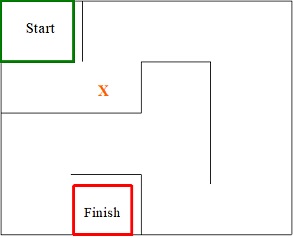
Figure 1 - sample maze

We can represent our maze as a 2D array (matrix) of Cells. Each Cell knows which of the four possible walls are adjacent to it. Each cell also knows if it is a starting or finishing cell. For example, in the maze shown in Figure 1, the top left hand corner cell (start) has walls to the top, left and right, but no wall below it, so we would be able to move from this cell to the cell below in a valid move. This cell would also have a flag to indicate that it is the starting cell. The maze in Figure 1 is a 4x4 maze with 16 cells.

We can simplify the above cell representation somewhat, such that, instead of a cell needing to know about the four directions around it each cell only needs to know if you can move to the cell to the right or to the cell down from it. This requires only 2 bits of information: Both closed (0) Right only open (1) Down only open (2) Both open (3). So our top left hand corner cell can be represented by the value 2 since we can only move down, and not to the right.

When we need to know about connectivity to cells above or to the left of us, we just need to look at their information. For instance, if I want to know about paths out of the cell in position 6 of the above maze (marked with an X) I know directly how it can move to the right or below. The data for this cell is 0 indicating it can't move to the right or down. To find if it can move to the top, I look at the data for cell 2 (the cell above it), which has value 3 indicating I can move both right and down from this cell. This also tells me that I can move up from cell 6. Similarly, I look to the value of cell to the left to know if I can move left from the current cell.

1. Generating a Random Maze

Although there are many techniques for generating mazes, we will focus on only one technique in this assignment. We will use a Depth First Search (DFS) technique to generate a random maze. The technique is as follows. To generate an n×m maze we create a grid graph of size n×m (for example, see Figure 2 for a 5x5 grid).

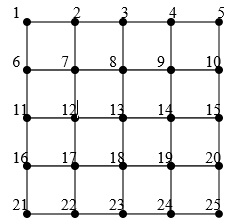
Figure 2 - sample 5x5 grid

To generate the maze, we mark a random vertex (vertex 1 in the top left corner in this example) as the start node, and then perform a DFS on the graph. When selecting which vertex to visit from the current node, we randomly select an unvisited node from the neighbouring vertices. For each edge that appears in our DFS tree, we consider this as a way to move from one cell to another in our resulting maze. Formulated another way, when two nodes are not connected by an edge in the DFS tree, then there is a wall between these two cells in the resulting maze. See Figure 3 for a sample DFS tree and resulting maze. Here the vertex labels indicate the order in which the nodes were visited in the DFS. The node that is the last one ‘visited' in our DFS is marked as the finish node (e.g., vertex 25, cell 3 in Figure 3).

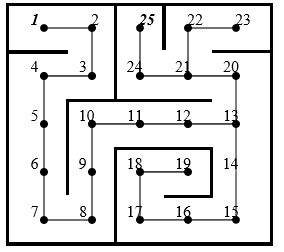
Figure 3 - sample maze generation

Your MazeGenerator program should ask the user for the size of the maze, based on the number of columns and rows and a file name for output. It should randomly generate a maze of this size. It will set the randomly visited first node as the start node, and the last node visited in the DFS as the finish node. Once the maze is generated, your program should save the maze to a file in the following format.

n,m:start_node:end_node:cell_openness_list

where
• start_node and end_node are not equal and are between 1 and n×m
• cell_openness values are decided by the following codes. 0: Both closed
1: Right only open 2: Down only open 3: both open

Example file format for the sample maze shown in Figure 3 would be:

5,5:1:3:1223030112231122230210110

2. Solving a Maze with DFS

Your second program MazeSolverDFS will input a maze from a file given as a command line argument in the format discussed above and solve it using a DFS. When solving a maze your program needs to keep track of order in which it visits the cells, and the numbers of steps taken to ‘walk' from start to finish. It will also keep track of the time taken to solve the maze. When selecting the next cell to visit, your program should always select the cell with the lowest grid number, as shown in Figure 2.

The program should output:
• The solution to the maze (path from start to finish). For example, looking at the path in Figure 4, the cell ordering is (1,2,7,6,11,16,21,22,17,12,13,14,15,10,9,4,5,4,9,8,3)
• The number of steps in this path. (For example, the number of steps is 20 for path given above). A step is a move from one cell to the next. Note that the sample solution contains a loop which is when a wrong path was taken, and we need to backtrack to then find the end point.
• The time taken to solve the maze, in milliseconds.

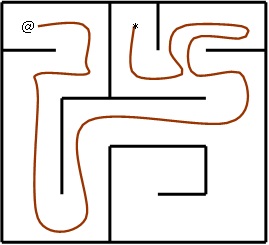
Figure 4 - sample maze solution path

3. Pairs only: Solving a Maze with BFS
If you are doing the assignment in pairs, your third program MazeSolverBFS will input a maze in the format discussed above and solve it using a BFS. Your program should produce the same output as for Task 2, that is:

• the solution to the maze from start to finish;
• the number of steps taken to find the finish;
• the time taken to solve the maze, in milliseconds.

4. Pairs only: Comparing the Two Techniques
To compare your two techniques for solving a maze, please produce the following data. Generate 5 random mazes for each of the following grid sizes.
• 20x20
• 20x50
• 100x100
For each maze you should also include maze.dat file containing the description of the maze in the format n,m:start_node:end_node:cell_openness_list.

Generate a table that compares the number of steps and time outputs, for each set of mazes, and for each method. Based on this data, write a very brief (50 words max) analysis of your results. That is, which method do you think performs better, and why?