Reference no: EM13524

A different smooth structure on R: Show that (U, Φ) given by

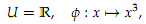
is a local chart of the topological manifold M = R which is not a member of the standard smooth structure on R. Now, consider the smooth atlas consisting of the one chart (U, Φ); this is a smooth atlas since the one chart covers all of R and since smooth compatibility is trivially satis?ed. This smooth atlas generates a smooth structure A on R. Let B be the standard smooth structure on R. Since A and B are distinct smooth structures, we get two distinct smooth manifolds (R, A) and (R, B). Now consider the map

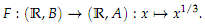
Show that it is a diffeomorphism.

This is an example of the following fundamental fact about smooth manifolds. A given topological manifold can carry many different smooth structures. In some cases, however, these smooth structures are "equivalent" in the sense that the resulting smooth manifolds are diffeomorphic. Indeed, one can show that there is only one smooth structure on R up to diffeomorphisms. More generally, all topological manifolds with dimension smaller or equal than 3 give rise to only one smooth structure up to diffeomorphisms. For dimensions larger than 3, this problem is partly unsolved. One knows that R⁴ can carry many "exotic" smooth structures, while all other Rⁿ have a unique smooth structure up to diffeomorphisms.

Problem 2

Consider the local chart (U, Φ) with where r, θ and Φ are the component functions of f. Determine the corresponding domain U ⊂ R³.

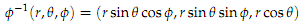
Hint: Recall that the standard smooth structure on R³ is generated by the smooth atlas which only consists of the one "global" chart ( ˜ U, Φ) with U = R³ and Φ = id discussed in the lecture. Hence the standard smooth structure is the set of all local charts on R3 which are smoothly compatible with ( ˜U, ˜Φ). Hence, in order to show that the local chart (U, Φ) above is in the standard smooth structure, we only need to show that it is smoothly compatible with ( ˜U, ˜Φ).