Reference no: EM13852131
1. The ancient Greek Democritus and his teacher Leucippus reasoned that matter must have a smallest component that was indivisible. Suppose you take one kilogram of gold and begin the process of dividing the material into successive halves. That is, you cut the gold into two half kilogram pieces; then you take one of the cut pieces and in turn cut it in half, and-so-on. How many cuts do you have to make before your last cut results in a single atom of gold? You must provide an algebraic solution.
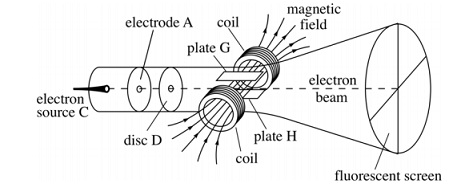
2. J.J. Thompson used the apparatus depicted in the diagram below to measure the ratio e/m. Electrons from source C move into the area between electrode A and disc D where they are accelerated by a potential of 100 Volts. After emerging from the small hole in plate D, they move into the velocity selector consisting of perpendicular electric and magnetic field. Plates G and H are separated by a distance of 1.0 cm and a potential of 50 Volts is applied across the plates. When the magnetic field is adjusted to a value of 0.00084 Tesla, the electron beam is observed to passes through the velocity filter undeviated.
a. Based on what you see in the diagram, should plate G be connected to thepositive or to the negative terminal of the 50 Volt power supply?
b. Based on the information given above, calculate the ratio of e/m.
c. Can you think of any reason why Thompson would not have used this approach to find e/m? ... seems a lot simpler!
3. In Millikan's experiment, an oil drop of radius 1.64 μm and density 0.851 g/cm3 is supended in a chamber between parallel plates when a downward electric field of 1.92 x105N/C is applied. Find the charge on the drop in terms of number of electrons.
4. Problem 23.91 (page 786 of the 13th edition of the textbook): The Milikan Oil Drop Experiment.