Calculating the compound interest formula

Reference no: EM1314244

The formula for computing the amount of money returned for an initial deposit into a bank account or CD (certificate of deposit) is given by:

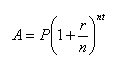
A is the amount of the return.

P is the principal amount initially deposited.

r is the annual interest rate (expressed as a decimal).

n is the number of compound periods in one year.

t is the number of years.

Carry all calculations to six decimals on each intermediate step, then round the final answer to the nearest cent.

Suppose you deposit $2,000 for 5 years at a rate of 8%.

[A.] Compute the return (A) if the bank compounds annually (n = 1).
[B.] Compute the return (A) if the bank compounds quarterly (n = 4). Final your answer to the nearest cent.
[C.] If a bank compounds continuously, then the formula used is A = pen
[D.] Does compounding annually or quarterly yield more interest? Explain why.
Where e is a constant & equals approximately 2.7183.

[E.] Compute A with continuous compounding. Round your answer to the nearest cent.
A commonly asked question is, “How long will it take to double my money?” At 8% interest rate & continuous compounding, what is the answer? Final your answer to the hundredth's place.

Reference no: EM1314244

Questions Cloud

Hypothesis test-analysis of variance : To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below.

Computation of the weighted average cost of capital : Computation of the weighted average cost of capital and Jake's Sound Systems has 210,000 shares of common stock outstanding at a market price of $36 a share

Hypothesis test for analysis of variance : The critical F value with 6 numerator and 60 denominator degrees of freedom at α = .05 is:

Preparation of bad debt account : Preparation of Bad debt Account and their Adjustment - What's the total f account in bad debts expense and What's the amount of the adjuster

Calculating the compound interest formula : Calculating the compound interest formula.

Objective type questions on capital budgeting : Objective type questions on capital budgeting and describe Chee Company has gathered the following data on a proposed investment project

Adjustment in general account balances : Adjustment in general account balances - Olsen Company has two office employees who earn $80 and $100 per day, respectively. They are paid each Friday for a five-day work week that begins each Monday. June 30 is a Tuesday in 2009.

Non parametric test-kruskal wallis test with box plots : Conduct post hoc comparisons with the LSD method. Which groups differ significantly at α = 0.05?

Determine cash payments for wages during the year : BLP Corporation reported wages expense of $224,000, wages payable of $89,400 at the beginning of the year and wages payable of $71,300 at the end of the year. Determine Cash payments for wages during the year

User Account

All Pages