Reference no: EM13163420

Write a C program (Care should be taken not to use extensions of C + + language in your work ) that calculates different formulas that converge to the number pi, to compare the speed of convergence of these formulas. Each form will be calculated by a different function. Each function will have the same parameter that indicates the number of terms to be used in the formula to approximate the value of the number pi. Here are the formulas that your program must calculate, in order of the speed convergence from the slowest to the fastest:

A) The first formula, very simple but the convergence is very slow, was discovered by Leonhard Euler:   

pi =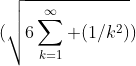       

Each partial sum E_k of this series can be expressed in terms of the first k terms, as follows:

Partial sum # 1 (first term): E1= sqrt(6)

Partial sum # 2 (first two terms): E2=sqrt(6)* sqrt(1+(1/4))

Partial sum # 3 (first three terms): E3= sqrt(6) * sqrt(1+(1/4)+(1/9))

Partial sum # 4 (first four terms): E4= sqrt(6)* sqrt(1+(1/4)+(1/9)+(1/16))

Etc.

B) The second formula, very elegant and discovered by William Brouncker is expressed as a continued fraction, but it is also very slow convergent

 

(4/pi) = 1 + (1² / 2 + (3² / 2 + (5² / 2 +( 7² / 2+ (9² / )

Each partial sum F_k of this series can be expressed in terms of the first k terms, as follows:

Partial sum # 1 (first term): F1= 1 + (1² /2 )

Partial sum # 2 (first two terms): F2= 1 + (1² /(2 + (3² / 2 )))

Partial sum # 3 (first three terms): F3= 1 + (1² /(2 + (3² / (2 +(5² /2) ) ) ) )

Partial sum # 4 (first four terms): F4= 1 + (1² /(2 + (3² / (2 +(5² /(2 + (7² / 2 ) ) ) ) ) ) )

Etc.

Note: Small suggestion to calculate the continued fraction, start with the last term, then continue with the penultimate term, and so on.

C) The third formula is still expressed as a continued fraction, with a slow convergence

 

(Pi/2) = 1 + (2 / (3+( (1*3)/ (4+ ((3*5)/ 4 +((5*7)/ 4+ ((7*9)/ )

 

Each partial sum F_k of this series can be expressed in terms of the first k terms, as follows:

Partial sum # 1 (first term): F1= 1 + (2 /3)

Partial sum # 2 (first two terms): F2= 1 + (2 /(3+ ((1*3)/4 )))

Partial sum # 3 (first three terms): F3= 1 + (2 /(3+ ((1*3)/(4+((3*5)/4 ) ) ) ) )

Partial sum # 4 (first four terms): F4= 1 + (2 /(3+ ((1*3)/(4+((3*5)/(4 +((5*7)/4) ) ) ) ) ) )

Etc.

Note: Small suggestion to calculate the continued fraction, start with the last term, then continue with the penultimate term, and so on.

D) The last formula, deduced from the arctan function and having a much faster convergence, was also discovered by Leonhard Euler:

pi =   \(\sum_{k=0}^{\infty} (2^{k} (k!)^{2}) / ((2k+1)! ) \)= 2 * (1+(1/3)+((1*2)/(3*5)) + ((1*2*3)/(3*5*7)) + ...)

Each partial sum E_k of this series can be expressed in terms of the first k terms, as follows:

Partial sum # 1 (first term): E₀= 2

Partial sum # 2 (first two terms): E1= 2 * (1+(1/3))

Partial sum # 3 (first three terms): E2= 2 * (1+(1/3)+((1*2)/(3*5)))

Partial sum # 4 (first four terms): E3= 2 * (1+(1/3)+((1*2)/(3*5)) + ((1*2*3)/(3*5*7)))

Etc.

Here are some partial results expected by your program outputs:

Convergence of the PI calculation with the first formula of Euler

Value with         1 terms = 2.4494897, error = 0.6921029

Value with         3 terms = 2.8577380, error = 0.2838546

Value with         7 terms = 3.0117739, error = 0.1298187

Value with         15 terms = 3.0793898, error = 0.0622028

Value with         23 terms = 3.1006973, error = 0.0408954

Value with         39 terms = 3.1173248, error = 0.0242679

etc.

 

Convergence of the PI calculation with the formula of Brouncker

Value with         1 terms = 2.6666667, error = 0.4749260

Value with         3 terms = 2.8952381, error = 0.2463546

Value with         7 terms = 3.0170718, error = 0.1245208

Value with         15 terms = 3.0791534, error = 0.0624393

Value with         23 terms = 3.0999440, error = 0.0416486

Value with         39 terms = 3.1165966, error = 0.0249961

etc.

 

Convergence of the PI calculation with the formula as continued fraction

Value with         1 terms = 3.33333333333333, error = 0.19174067974354

Value with         3 terms = 3.18095238095238, error = 0.03935972736259

Value with         5 terms = 3.15786435786436, error = 0.01627170427457

Value with         9 terms = 3.14710277682414, error = 0.00551012323435

Value with        13 terms = 3.14432869185326, error = 0.00273603826347

Value with        21 terms = 3.14267315437062, error = 0.00108050078083

etc.

 

Convergence of the PI calculation with the second formula of Euler

Value with        1 terms = 2.00000000000000, error = 1.14159265358979

Value with        3 terms = 2.93333333333333, error = 0.20825932025646

Value with        7 terms = 3.13215673215673, error = 0.00943592143306

Value with        11 terms = 3.14110602160138, error = 0.00048663198841

Value with        15 terms = 3.14156615934495, error = 0.00002649424484

Value with        19 terms = 3.14159116699150, error = 0.00000148659829

etc.

 

 

You will find that the values calculated by the program using a number of terms that are not consecutive ( for example, the first Euler's formula , one term , then 3 terms, and 7 terms used , etc. . ) . This phenomenon is explained by the irregularity algorithm used to determine the number of terms to compute. We start by calculating one term and is defined increments ( an integer variable ) set to 1 (as if you wanted to use two terms to the second iteration, then 3 terms in the third iteration, etc.). Calculating the absolute error of the current iteration and compared with the absolute error of the previous iteration : If this comparison reveals no significant new figure appeared, you double the increment . This iterative process continues until you get the desired number of significant digits .

For example, if the initial results of the first analysis Euler formula , we find that the second value uses three terms : indeed , the first value was not able to give a single significant digit of the number pi, we doubled the increment that increases from 1 to 2, and so the next iteration uses three terms (1 + increment value ) . According to the same principle as the second value has not brought a single new significant figure, we also doubled the increment which now goes from 2 to 4, and therefore the next iteration request under 7 (3 + value increment ) . And so on.

How does one decide whether a value provides a significant new number? Simply by comparing the integral part of the base 10 logarithm of the absolute error of the current iteration with the integer portion of the base 10 logarithm of the absolute error from the previous iteration . If these two quantities are identical, double- increment. Obviously, in the first iteration, there is no absolute error of the previous iteration , which is why we should initialize this amount to the value pi (which is quite logical since it is somewhat the maximum error we can have ) .

 

Note: To calculate the logarithm to the base 10, use the log10 function in the C library to get the integer part , you simply make an explicit conversion like this: (int) log10 ( yourvariable ) .

Now how do we decide the number of significant figures to calculate ? Simply by comparing the absolute error from the previous iteration with a precision chosen initially . Two cases are distinguished:

- For the first two formulas ( Euler and Bouncker ) which converge very slowly , a first precision 1e-7 should be used ( # define EPSILON1 1e- 7 )

- For the last two formulas , an accuracy of 1e- 14 is used ( # define EPSILON2 1e- 14)

Note: For the release of the first two options , use the conversion specification % 9d to print the number of terms used and the conversion specification % .7lf to print the value and error. For the release of the last two formulas , use the conversion specification % 7d to print the number of terms used and the conversion specification % .14lf to print the value and error.

Note : Use the following value for the number pi : # define PI 3.14159265358979

Note: Use the double type for your calculations because you need a fairly high accuracy.

In summary, your main function main() will consist of four almost identical loops to produce the results according to different formulas ( precision used, the function call to use and printing formats change, but the method is the same for all the loops ) . Each function must not call other