Reference no: EM13770
Calculate yield to maturity (YTM) and bond prices. A continuous compounding convention for YTM calculations should be used. The bond declaration may look something like:
class bond {
public:
bond() {}
~bond() {}
bond(double T0,double C0, double P0,double t0);
void set_price(double Price0);
double get_price();
void set_YTM(double YTM0);
double get_YTM();
double T;
double t;
double C;
double P;
private:
double Price;
double YTM;
};
You may also wish to include additional methods and attributes. The reason why the original time to maturity, T, the current time, t, the coupon payments, C, and the principal, P, are public fields, whereas the Price and Yield to maturity are defined as private fields is that the former are general attributes of a bond and can take on arbitrary (nonnegative) values, whereas the latter two are linked: one implies the other.
b) Create a method that calculates the bond price, given, YTM T, t, C and P.
c) Create a method that calculates the YTM, given Price, T, t, C and P.
d) Write a program that uses your class to calculate the YTM for a bond and the price of another bond. An example is shown below
e) Given parameters: T=10, t=0.75, C=4, P=100, YTM=0.045, what is the price of the bond?
f) Given parameters: T=25, t=0.5, C=80, P=1000, Price=1010, what is the (continuously compounded) YTM of the bond? Use your program to calculate the answer.
2. Term structure
Since there are only a finite number of bonds available in the market. There will always be "holes" to fill in when defining a yield curve in continuous time. A common approach is to define a parameterized set of possible yield curves, and choose a curve within this set that provides a good approximation of the yields of observed bonds. There are many ways to choose such a parameterized set and to define what is meant by a "good approximation." You can read a book on term structure estimation if you are interesting in learning more.
In this exercise, we will use the Nelson-Siegel parametric class of term structures
The Nelson
Siegel model defines a set of zero-coupon yield curves, defined by five parameters, as described in class, i.e., the yield of a zero coupon bond of maturity T is y(T|A), where A = {β1, β2, β3, λ1,λ2}
where ={).The model has been covered in class.
A "good approximation" is now defined in the least square sense. Assume that there are n bonds available, with observed prices P1...Pn. Given the Nelson-Siegel yield curve y(T|A), the price would be ?? ^??(Λ). The residual between observed and estimated prices is then
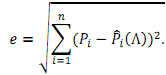
The yield curve that minimizes this residual is the so-called least square solution. In other words the parameter set, is chosen to minimize the residual e, leading to the yield curve y(T|). This is the yield curve we will model in this exercise.
a) Design a term structure class, call it TermStructure, based on the Nelson-Siegel term structure. An object is defined by its attributes, and there should be methods for calculating:
a. The yield at any positive maturity
b. The short rate
c. The forward rate, F(S,T).
Of course, the class needs constructors, destructors and ways to reach its attributes. Store the class declaration in a file called TermStructure.h and the class implementation in TermStructure.cpp
b) Add a method that takes a bond and calculates its price, given the Nelson-Siegel yield curve, with parameters.
c) Write a program that shows how a) and b) work. For example, the program could do the following
d) What is the price of the bond given in the previous figure, when the Nelson-Siegel parameters =1 are chosen?
e) Estimation of the yield curve using nonlinear least squares minimization: The last part of this assignment asks you to construct the Nelson Siegel yield curve from observed bond prices, by minimizing the mean squared error.