Reference no: EM13197459
Following is information for the required returns and standard deviations of returns for A, B, and C.
Here are the expected returns and standard deviations for stocks A, B, and C:
| Here are the expected returns and standard deviations for stocks A, B, and C: |
| Stock |
ri |
si |
|
|
| A |
7.0% |
33.11% |
|
|
| B |
10.0% |
53.85% |
|
|
| C |
20.0% |
89.44% |
|
|
| |
A |
B |
C |
| A |
1.0000 |
0.1571 |
0.1891 |
| B |
0.1571 |
1.0000 |
0.1661 |
| C |
0.1891 |
0.1661 |
1.0000 |
a. Suppose a portfolio has 30 percent invested in A, 50 percent in B, and 20 percent in C. What are the expected return and standard deviation of the portfolio?
| wA = |
30% |
| wB = |
50% |
| wC = |
20% |
|
|
| rp = |
|
Hint: for the portoflio standard deviation, start by creating a table like the one in Section 3.1 for the N-asset case. In fact, begin by creating a table with the products of the weights and standard deviations for each pair of stocks. If you are careful about how you construct the formulas, you can copy them. Then take the results from this intermediate table and multiply them by the correlations above.
|
|
|
|
A |
B |
C |
|
|
|
wi = |
30% |
50% |
20% |
|
|
|
si = |
33.11% |
53.85% |
89.44% |
|
|
|
wi x si = |
|
|
|
|
wi |
si |
wi x si |
|
|
|
| A |
30% |
33% |
|
|
|
|
| B |
50% |
54% |
|
|
|
|
| C |
20% |
89% |
|
|
|
|
|
|
|
|
|
|
|
| Now multiply the products of wi x si x wj x sj by the correlations given above to create a table like the one in Section 3.1. |
A |
|
|
|
| B |
|
|
|
| C |
|
|
|
b. The partial model lists 66 different combinations of portfolio weights. For each combination of weights, find the required return and standard deviation.
| Portoflio # |
wA |
wB |
wC |
Variance |
sp |
rp |
| 1 |
0.0 |
0.0 |
1.0 |
|
|
|
| 2 |
0.0 |
0.1 |
0.9 |
|
|
|
| 3 |
0.0 |
0.2 |
0.8 |
|
|
|
| 4 |
0.0 |
0.3 |
0.7 |
|
|
|
| 5 |
0.0 |
0.4 |
0.6 |
|
|
|
| 6 |
0.0 |
0.5 |
0.5 |
|
|
|
| 7 |
0.0 |
0.6 |
0.4 |
|
|
|
| 8 |
0.0 |
0.7 |
0.3 |
|
|
|
| 9 |
0.0 |
0.8 |
0.2 |
|
|
|
| 10 |
0.0 |
0.9 |
0.1 |
|
|
|
| 11 |
0.0 |
1.0 |
0.0 |
|
|
|
| 12 |
0.1 |
0.0 |
0.9 |
|
|
|
| 13 |
0.1 |
0.1 |
0.8 |
|
|
|
| 14 |
0.1 |
0.2 |
0.7 |
|
|
|
| 15 |
0.1 |
0.3 |
0.6 |
|
|
|
| 16 |
0.1 |
0.4 |
0.5 |
|
|
|
| 17 |
0.1 |
0.5 |
0.4 |
|
|
|
| 18 |
0.1 |
0.6 |
0.3 |
|
|
|
| 19 |
0.1 |
0.7 |
0.2 |
|
|
|
| 20 |
0.1 |
0.8 |
0.1 |
|
|
|
| 21 |
0.1 |
0.9 |
0.0 |
|
|
|
| 22 |
0.2 |
0.0 |
0.8 |
|
|
|
| 23 |
0.2 |
0.1 |
0.7 |
|
|
|
| 24 |
0.2 |
0.2 |
0.6 |
|
|
|
| 25 |
0.2 |
0.3 |
0.5 |
|
|
|
| 26 |
0.2 |
0.4 |
0.4 |
|
|
|
| 27 |
0.2 |
0.5 |
0.3 |
|
|
|
| 28 |
0.2 |
0.6 |
0.2 |
|
|
|
| 29 |
0.2 |
0.7 |
0.1 |
|
|
|
| 30 |
0.2 |
0.8 |
0.0 |
|
|
|
| 31 |
0.3 |
0.0 |
0.7 |
|
|
|
| 32 |
0.3 |
0.1 |
0.6 |
|
|
|
| 33 |
0.3 |
0.2 |
0.5 |
|
|
|
| 34 |
0.3 |
0.3 |
0.4 |
|
|
|
| 35 |
0.3 |
0.4 |
0.3 |
|
|
|
| 36 |
0.3 |
0.5 |
0.2 |
|
|
|
| 37 |
0.3 |
0.6 |
0.1 |
|
|
|
| 38 |
0.3 |
0.7 |
0.0 |
|
|
|
| 39 |
0.4 |
0.0 |
0.6 |
|
|
|
| 40 |
0.4 |
0.1 |
0.5 |
|
|
|
| 41 |
0.4 |
0.2 |
0.4 |
|
|
|
| 42 |
0.4 |
0.3 |
0.3 |
|
|
|
| 43 |
0.4 |
0.4 |
0.2 |
|
|
|
| 44 |
0.4 |
0.5 |
0.1 |
|
|
|
| 45 |
0.4 |
0.6 |
0.0 |
|
|
|
| 46 |
0.5 |
0.0 |
0.5 |
|
|
|
| 47 |
0.5 |
0.1 |
0.4 |
|
|
|
| 48 |
0.5 |
0.2 |
0.3 |
|
|
|
| 49 |
0.5 |
0.3 |
0.2 |
|
|
|
| 50 |
0.5 |
0.4 |
0.1 |
|
|
|
| 51 |
0.5 |
0.5 |
0.0 |
|
|
|
| 52 |
0.6 |
0.0 |
0.4 |
|
|
|
| 53 |
0.6 |
0.1 |
0.3 |
|
|
|
| 54 |
0.6 |
0.2 |
0.2 |
|
|
|
| 55 |
0.6 |
0.3 |
0.1 |
|
|
|
| 56 |
0.6 |
0.4 |
0.0 |
|
|
|
| 57 |
0.7 |
0.0 |
0.3 |
|
|
|
| 58 |
0.7 |
0.1 |
0.2 |
|
|
|
| 59 |
0.7 |
0.2 |
0.1 |
|
|
|
| 60 |
0.7 |
0.3 |
0.0 |
|
|
|
| 61 |
0.8 |
0.0 |
0.2 |
|
|
|
| 62 |
0.8 |
0.1 |
0.1 |
|
|
|
| 63 |
0.8 |
0.2 |
0.0 |
|
|
|
| 64 |
0.9 |
0.0 |
0.1 |
|
|
|
| 65 |
0.9 |
0.1 |
0.0 |
|
|
|
| 66 |
1.0 |
0.0 |
0.0 |
|
|
|
Hint: Use the formula to calculate the variance for each portfolio and then copy it down. This formula should have six values in it: 1 for Stock A, 1 for Stock B, 1 for Stock C, one for the cross-term of A and B, 1 for the cross-term of A and C, and 1 for the cross term of B and C. The results for portfolio #36 should match your results in part a.
c. The partial model provides a scatter diagram (shown below) showing the required returns and standard deviations calculated above. This provides a visual indicator of the feasible set. If you would like a return of 10.50 percent, what is the smallest standard deviation that you must accept?
For rp = 10.50%, the smallest (and the only) standard deviation is 33.87%; see portfolio #49.
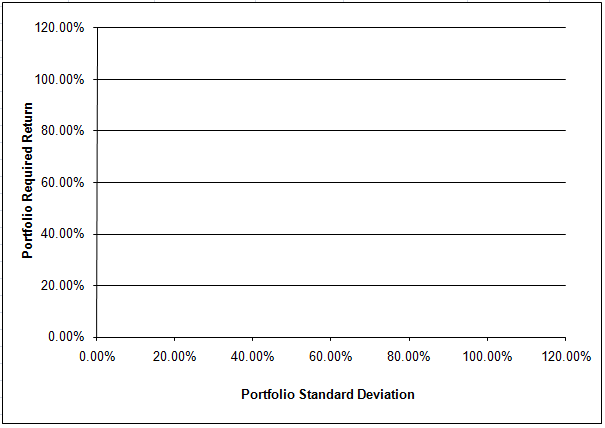
|
What does proportional representation means
: Proportional representation means that the candidate who gets the most votes in an election wins. party that gets 51 percent takes all of the available seats. number of seats a party gets is in proportion to its percentage of the vote.
|
|
Estimate the maximum error in the calculated surface area
: The circumference of a sphere was measured to be 70.000 cm with a possible error of 0.50000 cm. Use linear approximation to estimate the maximum error in the calculated surface area.
|
|
Managing our time is so fundamental that we hardly notice
: Managing our time is so fundamental that we hardly notice it. However, every single day we make dozens of decisions about what we want to accomplish during that day and what we decide to do next, and then next, and then next...etc. All those indiv..
|
|
What temperature represents the 95th percentile
: The body temperatures of adults are normally distributed with a mean of 98.6° F and a standard deviation of 0.44° F. What temperature represents the 95th percentile?
|
|
Calculate the variance for portfolio
: Calculate the variance for each portfolio and then copy it down. This formula should have six values in it: 1 for Stock and what is the smallest standard deviation that you must accept?
|
|
Find the overhead and the marginal cost of a figurine
: A manufacturer of small glass figurines discovers that it costs $ 1800 for a production run of 1600 and $ 1900 for a production run of 1800 . Assuming that cost is a linear function of the number of items, find the overhead and the marginal cost o..
|
|
State the toolwire landscape
: I've had the toolwire landscape try, they could not help me. I had the techology support do a complete check of my computer, and still could not find nothing. I need help.
|
|
Define what famous playwright is wakako yamauchi''s plays
: What famous playwright is Wakako Yamauchi's plays compared to because of the small but precisely chosen details with which she renders her characters lives and the quiet anguish that the characters express?
|
|
Give equations fo find equilibrium
: Assume that the equation for demand for bread at a small bakery is Qd = 60 - 10Pb + 3Y If Y is 10 and Pf is $1, solve mathematically for equilibrium Q and Pb.
|