Reference no: EM13123366
(1) Prove the following vector calculus identity in R3, where f is a twice continuously di erentiable scalar eld and F is a twice continuously di erentiable vector fi eld:
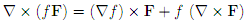
(2) Let F(x; y; z) = (y + z)i + (x + z)j + (x + z)k. The sphere x2 + y2 + z2 = a2 intersects the postive x-, y-, and z-axes at points A, B, and C, respectively. The simple closed curve K consists of the three circular arcs AB, BC, and CA. Let S denote the surface ABC of the octant of the sphere bounded by K, oriented away from the origin. Let T denote the unit tangent vector to K, and n the unit normal vector to S.
(a) Calculate the line integral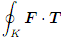 
ds directly without using Stokes' Theorem.
(b) Calculate the surface integral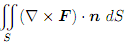 
without using Stokes' Theorem.
(3) Consider the matrix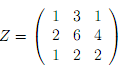 
(a) Find a PLU decomposition for the matrix Z.
(b) Use your answer to part (a) to solve the system of equations
x + 3y + z = 1;
2x + 6y + 4z = 4;
x + 2y + 2z = 6:
(4) Consider the matrix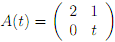 
(a) Find the eigenvalues and eigenvectors of A(t).
(b) For which values of t will A(t) be diagonalisable? Explain.
(c) For those values of t from part (b), nd an invertible matrix P(t) and a diagonal matrix D(t) such that A(t) = P(t)D(t)P(t)-1.
(d) Give a formula for A(t)n (where n is a positive integer) that holds for those values of t from part (b).
|
Calculate the molarity of each of the given solutions
: Calculate the molarity of each of the following solutions. (a) 23.0 g of ethanol (C2H5OH) in 545 mL of solution (b) 15.4 g of sucrose (C12H22O11) in 74.0 mL of solution
|
|
Highlighting the part indicated by given interval
: Find a definite integral that represents the arc length of the curve over the indicated interval and observe that the length cannot be evaluated with the techniques studied so far
|
|
How to conclude proportion has indeed changed
: School seniors in his random sample, 159 believe that "getting rich" is an important goal. Can he conclude, at the 0.05 level of significance, that the proportion has indeed changed?
|
|
What is the molarity of a solution of vinegar
: What is the molarity of a solution of vinegar that is 5.00 % by mass acetic acid (CH3CO2H) and has a density of 1.01 g/mL.
|
|
Calculate the surface integral
: Prove the following vector calculus identity in R 3 , where f is a twice continuously di erentiable scalar eld and F is a twice continuously di erentiable vector fi eld
|
|
Hamiltonian graphs and connected graphs
: Show that if G is a 2-connected graph containing a vertex that is adjacent to at least three vertices of degree 2, then G is not hamiltonian.
|
|
Common stock outstanding of landon corporation
: On January 1, 2010, Garner Corporation purchased 25% of the common stock outstanding of Landon Corporation for $250,000. During 2010, Landon Corporation reported net income of $80,000 and paid cash dividends of $40,000.
|
|
Find minimum sample size to assure estimate of p
: The required margin of error around the population p. Margin of error: 0.09; confidence level: 95%; from a prior study, p is estimated by the decimal equivalent of 87%.
|
|
Interest in the stock of finley corporation
: Nance Company owns 30% interest in the stock of Finley Corporation. During the year, Finley pays $25,000 in dividends to Nance, and reports $100,000 in net income. Nance Company's investment in Finley will increase by
|