Reference no: EM131878924

Part A -

1. Assume a matrix T (that transforms probability densities) is given by

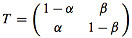
(a) Calculate the determinant, Δ, of the matrix T, i.e., Δ = det T.

(b) Calculate the eigenvalues, λ₁ and λ₂, of T as a function of Δ.

(c) Assume the eigenvectors v₁ and v₂, corresponding the eigenvalues λ₁ and λ₂ respectively, are written as

calculate the parameters a and b.

(d) Normalize v₁ and v₂ such that their "lengths" are 1, i.e., v₁₁² + v₂₁² = 1 + a² = 1 for v₁ while vie v₁₂² + v₂₂² = b² +1 = 1 for v₂.

(e) Normalize v₁ and v₂ such that their "sums" are 1, i.e., 1 + a = 1 for v₁ while b + 1 = 1 for v₂.

(f) Write the matrix Λ (for the eigenvalues) as

and the matrix V (for the eigenvectors) as

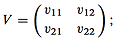
and show that the two eigen equations can be written as

T V =V Λ,

(g) Assuming the vectors are normalized according to (e), calculate the inverse of V, i.e., V^-1.

Part B -

1. A box contains 5 R balls, 3 W balls, and 2 B balls. The event X_i represents the ball designated in the process of selecting a ball from the box, noting the ball, and returning the ball to the box. Thus, the set Xx_i = {R, W, B), with probabilities Px_i = (p, q, r} = {0.5, 0.3, 0.2). An iid process consist of a sequence X₁, X₂, ... X₈.

(a) Calculate the entropy

H₃ (p, q) = -p log p - q log q -(1 - p - q) log(1 - p - q),

(b) Calculate the range of probabilities of the joint density p(X₁, X₂, . . .X₈).

(c) Calculate the range of joint densities for the members of the typical set A_∈⁽⁸⁾, for ∈ = 0.1, 0.5, and 1.

(d) Calculate the mass density of the typical set for the three values of ∈.