Reference no: EM132341845

Assignment

Question 1 : In basketball, points are scored by a successful free throw or a field goal. A successful free throw is worth 1 point while a field goal is worth either 2 or 3  points. An attempt can either be a free throw attempt or a field goal attempt.

In the recently concluded basketball season, Stephen had 1695 attempts in total. 60% of these attempts were successful and he scored a total of 1917 points. 40% of his successful free throws and 25% of his field goal points were scored during the second half of the season, where Stephen scored a total of 534 points.

Calculate the number of 2-point field goals during the season.

Question 2 : A cylinder is inscribed in a cone as shown in the diagram below. The cone has a height of 8 cm and a fixed radius of R cm. The cylinder has a radius of x cm and a height of h cm.

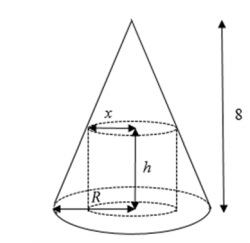
Show that th e volume of the cylinder is maximised when x = kR, where k is a constant to be determined.

Question 3 : A curve C has equation

y = ((3x²+3x-22) / (x²+x-2))
(i) Sketch the curve C, labelling any points where C crosses the x- and y- axes, the coordinates of the turning point and the equations of the asymptotes.

(ii) State the range of values of x for which C is concave downwards. Hence, solve the inequality

e^{((3x2+3x-22) / (x2+x-2))} < x - 2

Question 4 :

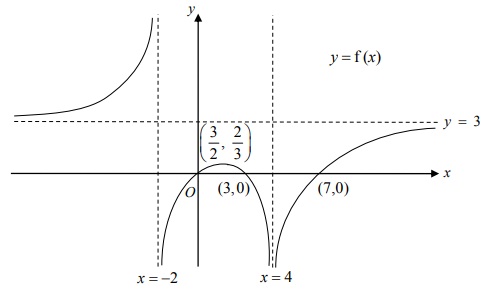
The diagram above shows the curve y = x(f) . The curve crosses the x-axis at (0,0) , (3,0) and (7,0). It has a turning point at ((3/2), (2/3)) and the lines y = 3 , x= -2 and x = 4 are asymptotes to the curve.

Sketch, on separate diagrams, the graphs of

(i) y = 1 + f(-x) ,

(ii) y =  f'(x).

Label clearly the coordinates of any turning points, the equations of any asymptotes and the points where the graphs intersect the axes where appropriate.

Question 5 : Relative to the origin O, the points A, B and C have position vectors given respectively by

2i – 4j + 3k, 3i +2j – k and (2 + p)i + (1 - 2p)j + pk, where p is real.

(a) Determine the angle AOB.              

(b) Find the values of p for which OC = AB.

(c) The point Q is on AB produced such that AB: BQ is 2:7. Find the position vector of the point Q and the unit vector in the direction of (OQ)‾  Leave your answers in exact form.

Question 6 :  Prove by the method of differences that

Σⁿ_r=2 ln [ r²/((r-1)(r+1)) ] = ln2+ln(n/(n+1))

Hence, find the least value of integer k such that

Σ^∞_r=2 ln [ r²/((r-1)(r+1)) ] < 0.01.

Question 7 : The diagram below shows a shaded region which is bounded by the curve C with equation

y = sec x tan³ x and the line L with equation

y = (4√2/Π) x.

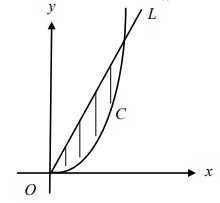
(i) Verify that the point (π/4 , √2) lies on both C and L.

(ii) Find the exact volume of the solid generated by revolving the shaded region about the x-axis through 2π . Express your answer in the form 1/42(aπ²-bπ), where a and b are integers.

Question 8 : In a chemical laboratory, the amount of substance X in a chemical reaction is being measured. The mass of substance X, in g at any time t minutes after the start of the chemical reaction is denoted by x and it satisfies the differential equation
(dx/dt = 1-x²) .

The mass of substance X is 1.5 g at the start of the chemical reaction.

(i) Find the particular solution, obtaining an expression for x in terms of t.

(ii) What happens to the amount of substance X in the long run?

(iii) Sketch a graph to show how the amount of substance X varies with time, labelling the point where the graph intersects the axis and the equation of the asymptote.

9 The functions f and g are defined by

f : x |→  |3-2x|, for x ∈ R, 0 ≤ x ≤  2,

g : x |→ cos ((π/4)x), for x ∈ R, 1 ≤ x ≤  2

(i) Sketch the graph of y = f(x) and state the exact range of f.

(ii) Find g^-1 (x) and write down the exact domain and range of g^-1 .

(iii) Show that the composite function 1 fg^-1 exists and find the range of fg^-1 .

Question 10 : (a) John owes the bank $20 000 on 1 January 2016. The bank offers him two types of financial schemes to repay his debt.

Scheme 1: At the start of every month, interest is added to the amount he owes at a fixed rate of 0.4% of the outstanding amount. At the end of every month, John makes a payment of $500.

Scheme 2: At the start of every month, a fixed interest of $75 is charged to the amount he owes. At the end of every month, John makes a payment of $500.

(i) If John were to take up Scheme 1, show that the amount of money he would owe the bank at the end of the n^th month is 

125000 - (105000) 1.004ⁿ.

(ii) John wants to pay off his debt in the shortest time. Which scheme should he take up? Justify your choice.

(b) The sum of the first 30 terms of an arithmetic progression with a non-zero common difference is 300. Given that the first, third and thirteenth terms of the arithmetic progression are consecutive terms of a geometric progression, find the first term and common difference of the arithmetic progression, and determine whether the sum to infinity of the geometric progression exists.

Question 11 : The curve C has parametric equations

x = 1+e^t, y=2t for t ∈ R.

(i) Sketch C, labelling any intersections between C and the axes.

(ii) Show that the tangent to the curve at t = 1, denoted by l, has equation

y = (2/(1+e))x.

(iii) Find the exact value of  _-1∫¹w(1+e^w)dw

Hence, find the exact area bounded by the curve C, the lines l and x=-1+e^-1 .

Question 12 : A Lorenz curve is given by

y = L(x), where 0 ≤ x ≤  1 and 0 ≤ y ≤ 1 .

y represents the proportion of a country’s total wealth that is owned by the poorest 100x% of the country’s population in terms of wealth.

C is a Lorenz curve with equation

L₁(x) = (2/π) sin^-1 x

(a) Find the percentage of total wealth owned by the poorest 20% of the population.

(b) A power series is used to approximate L₁(x).

(i) Find the series expansion of L₁(x) up to and including the term in x³ .

(ii) Hence, find the range of values of x such that the error of approximating L₁(x) using its series expansion in part (b) (i) is less than or equal to 0.005.

(c) The information in the Lorenz curve is often summarised as an index to measure the distribution of wealth in a population. This index is called the Gini Index.

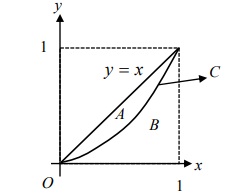
With reference to the diagram above, the Gini Index for C is defined as follows.

Let A be the area of the region bounded by the line y = x and C . Let B be the area of the region bounded by C , the x-axis and the line

x = 1 .

The Gini Index for C is evaluated as (A/(A+B)).

(i) Find the Gini Index for C, correct to 3 significant figures.

(ii) Explain whether populations with the same Gini Index must have the same Lorenz curve.